Samobalansujący robot wykorzystujący algorytm PID (STM MC): 9 kroków

2024 Autor: John Day | [email protected]. Ostatnio zmodyfikowany: 2024-01-30 11:31

Ostatnio dużo pracy wykonano w zakresie samobalansowania obiektów. Koncepcja samobalansowania zaczęła się od zrównoważenia odwróconego wahadła. Koncepcja ta rozszerzyła się również na projektowanie samolotów. W tym projekcie zaprojektowaliśmy mały model robota samobalansującego z wykorzystaniem algorytmu PID (Proportional, Integral, Derivative). Od tego czasu ta metoda jest nowym obliczem systemów sterowania procesami przemysłowymi. Ten raport zawiera przegląd metod związanych z samobalansowaniem obiektów. Projekt ten był realizowany jako projekt semestralny w celu zrozumienia korelacji PID z wydajnością różnych procesów przemysłowych. Tutaj skupiamy się jedynie na przedstawieniu krótkiego przeglądu skuteczności i zastosowania regulacji PID. Niniejszy dokument został opracowany przez dostarczenie krótkiego wprowadzenia do systemów sterowania i związanych z nimi terminologii, wraz z motywacją projektu. Przeprowadzono eksperymenty i obserwacje, opisano zalety i wady kończąc na przyszłych ulepszeniach. Opracowano model robota samobalansującego, aby zrozumieć skuteczność PID w świecie systemów sterowania. Przechodząc przez rygorystyczne testy i eksperymenty, odkryto zalety i wady systemu regulacji PID. Stwierdzono, że pomimo wielu zalet sterowania PID w stosunku do dotychczasowych metod, nadal system ten wymaga wielu usprawnień. Mamy nadzieję, że czytelnik dobrze zrozumie znaczenie samorównoważenia, skuteczność i braki regulacji PID

Krok 1: Wprowadzenie

Wraz z pojawieniem się komputerów i uprzemysłowieniem procesów, w całej historii ludzkości zawsze prowadzono badania mające na celu opracowanie sposobów udoskonalania procesów i, co ważniejsze, kontrolowania ich za pomocą autonomicznych maszyn. Celem jest zmniejszenie zaangażowania człowieka w te procesy, a tym samym zmniejszenie błędu w tych procesach. Stąd powstał Kierunek „Inżynieria Systemów Sterowania”. Inżynierię Systemów Kontroli można zdefiniować jako stosowanie różnych metod do kontrolowania pracy procesu lub utrzymywania stałego i preferowanego środowiska, zarówno ręcznego, jak i automatycznego.

Prostym przykładem może być kontrolowanie temperatury w pomieszczeniu. Sterowanie ręczne oznacza obecność w obiekcie osoby, która sprawdza zastane warunki (czujnik), porównuje je z pożądaną wartością (przetwarzanie) i podejmuje odpowiednie działania w celu uzyskania żądanej wartości (siłownik). Problem z tą metodą polega na tym, że nie jest ona bardzo niezawodna, ponieważ osoba jest podatna na błędy lub zaniedbania w swojej pracy. Kolejnym problemem jest to, że tempo procesu inicjowanego przez siłownik nie zawsze jest jednorodne, co oznacza, że czasami może przebiegać szybciej niż jest to wymagane, a czasami może być wolniejsze. Rozwiązaniem tego problemu było zastosowanie mikrokontrolera do sterowania systemem. Mikrokontroler jest

zaprogramowany do sterowania procesem, zgodnie z podanymi specyfikacjami, połączony w obwód (do omówienia później), zasilany pożądaną wartością lub warunkami i tym samym steruje procesem w celu utrzymania pożądanej wartości. Zaletą tego procesu jest to, że w tym procesie nie jest wymagana interwencja człowieka. Również tempo procesu jest równomierne

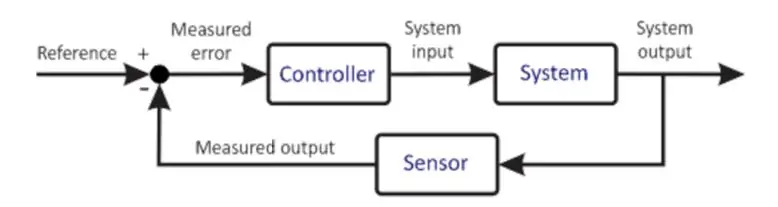
Podstawowy system sterowania

Poprzedni diagram przedstawia bardzo uproszczoną wersję Systemu Kontroli. Mikrokontroler jest sercem każdego systemu sterowania. Jest to bardzo ważny element, dlatego jego dobór powinien być starannie dokonany w oparciu o wymagania Systemu. Mikrokontroler otrzymuje dane wejściowe od użytkownika. Wejście to określa pożądany stan systemu. Mikrokontroler otrzymuje również sygnał zwrotny z czujnika. Czujnik ten jest podłączony do wyjścia Systemu, którego informacje są zwracane na wejście. Mikroprocesor na podstawie swojego programowania wykonuje różne obliczenia i podaje sygnał wyjściowy do siłownika. Siłownik w oparciu o moc steruje instalacją, starając się utrzymać te warunki. Przykładem może być sterownik silnika napędzający silnik, gdzie sterownik silnika jest siłownikiem, a silnik jest instalacją. Silnik obraca się zatem z określoną prędkością. Podłączony czujnik odczytuje aktualny stan instalacji i przesyła go z powrotem do mikrokontrolera. Mikrokontroler ponownie porównuje, wykonuje obliczenia i cykl się powtarza. Ten proces jest powtarzalny i nieskończony, dzięki czemu mikrokontroler utrzymuje pożądane warunki

Krok 2: System sterowania oparty na PID

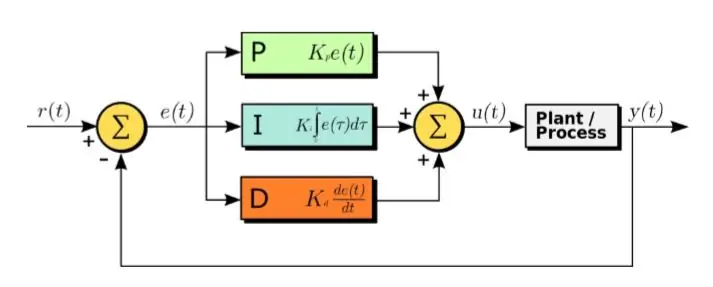
Algorytm PID jest skuteczną metodą projektowania Systemu Sterowania.

Definicja

PID oznacza proporcjonalny, całkowy i pochodny. W tym algorytmie sygnałem wejściowym jest otrzymany sygnał błędu. A następujące równanie jest stosowane do sygnału błędu:

U(t) = Kp∗e(t) + Kd∗d/dt(e(t)) + Ki∗całka(e(t)) (1.1)

Krótkie wyjaśnienie

Jak widać z powyższego równania, całka i pochodna sygnałów błędu są obliczane, mnożone przez ich odpowiednie stałe i dodawane wraz ze stałą Kp pomnożoną przez e(t). Wyjście jest następnie podawane do siłownika, który uruchamia system. Teraz spójrzmy po kolei na każdą część funkcji. Ta funkcja ma bezpośredni wpływ na czas narastania, czas opadania, szczytowe przekroczenie, czas ustalania i błąd stanu ustalonego.

• Część proporcjonalna: Część proporcjonalna skraca czas narastania i zmniejsza błąd stanu ustalonego. Oznacza to, że system potrzebuje mniej czasu, aby osiągnąć swoją wartość szczytową, a gdy osiągnie stan ustalony, błąd stanu ustalonego będzie niski. Zwiększa jednak przeregulowanie szczytu.

• Część pochodna: Część pochodna redukuje przeregulowanie i czas ustalania. Oznacza to, że stan przejściowy systemu będzie bardziej tłumiony. Ponadto system osiągnie stan ustalony w krótszym czasie. Jednak nie ma to żadnego wpływu na czas narastania lub błąd stanu ustalonego.

• Część integralna: Część integralna skraca czas narastania i całkowicie eliminuje błąd stanu ustalonego. Zwiększa jednak przeregulowanie szczytowe i czas ustalania.

• Strojenie: Dobry system sterowania będzie charakteryzował się niskim czasem narastania, czasem ustalania, przeregulowaniem wartości szczytowej i błędem stanu ustalonego. Dlatego Kp, Kd, Ki muszą być precyzyjnie dostrojone, aby dostosować udział powyższych czynników w celu uzyskania dobrego systemu sterowania.

Załączony rysunek przedstawiający efekt zmiany różnych parametrów w algorytmie PID.

Krok 3: samobalansujący robot

Robot samobalansujący to wielowarstwowy robot dwukołowy.

Robot będzie próbował się zrównoważyć po przyłożeniu dowolnej nierównej siły. Zrównoważy się poprzez przyłożenie siły przeciwnej wypadkowej sił działających na robota.

Metody samobalansowania

Istnieją cztery metody samobalansowania robotów. Są to następujące:

Samobalansowanie za pomocą dwóch czujników nachylenia IR

Jest to jeden z najbardziej prymitywnych sposobów zrównoważenia robota, ponieważ wymaga mniej sprzętu i stosunkowo łatwego algorytmu. W tym podejściu do pomiaru odległości między ziemią a robotem wykorzystywane są dwa nachylone czujniki podczerwieni. W oparciu o obliczoną odległość, PID może być używany do napędzania silników w celu odpowiedniego wyważenia robota. Wadą tej metody jest to, że czujnik podczerwieni może przeoczyć niektóre odczyty. Innym problemem jest to, że do obliczenia odległości wymagane jest przerwanie i pętle, co zwiększa złożoność czasową algorytmu. Stąd ta metoda wyważania robota jest mało efektywna.

Samobalansowanie za pomocą akcelerometru

Akcelerometr podaje nam przyspieszenie ciała w 3 osiach. Przyspieszenie zorientowane w osi y (do góry) i osi x (do przodu) daje nam miarę do obliczenia kierunku grawitacji, a tym samym obliczenia kąta nachylenia. Kąt oblicza się w następujący sposób:

θ = arctan (Ay/Ax) (1,2)

Wadą stosowania tej metody jest to, że podczas ruchu robota do odczytów dodawane będzie również przyspieszenie poziome, które jest szumem o wysokiej częstotliwości. Stąd kąt nachylenia będzie niedokładny.

Samobalansowanie za pomocą żyroskopu

Żyroskop służy do obliczania prędkości kątowych wzdłuż trzech osi. Kąt nachylenia uzyskuje się z następującego równania.

θp(i) = θp(i−1) + 1/6(vali−3 + 2vali−2 + 2vali−1 + vali) (1,3)

Dużą wadą korzystania z żyroskopu jest to, że ma on małe odchylenie prądu stałego, które jest szumem o niskiej częstotliwości i po kilku chwilach zwracane wartości są całkowicie błędne. To po integracji spowoduje odsunięcie punktu zerowego. W rezultacie robot przez pewien czas pozostanie w pozycji pionowej i przewróci się, gdy nadejdzie dryf.

Samobalansowanie za pomocą akcelerometru i żyroskopu

Jak wspomniano powyżej, używanie tylko akcelerometru lub żyroskopu nie da nam prawidłowego kąta nachylenia. Aby to uwzględnić, stosuje się zarówno akcelerometr, jak i żyroskop. Oba są wbudowane w MPU6050. W ten sposób uzyskujemy dane od obu z nich, a następnie łączymy je za pomocą filtru Kalmana lub filtru komplementarnego.

• Filtr Kalmana: Filtr Kalmana oblicza najlepsze oszacowanie stanu systemu dynamicznego na podstawie zaszumionych pomiarów, minimalizując średni kwadratowy błąd oszacowania. Działa w dwóch etapach, przewidywania i korekcji, biorąc pod uwagę dyskretne równania stochastyczne opisujące dynamikę systemu. Jest to jednak bardzo złożony algorytm, który można zaimplementować zwłaszcza na ograniczonym sprzęcie mikrokontrolera.

• Filtr komplementarny: Algorytm ten wykorzystuje przede wszystkim dane uzyskane z żyroskopu i integruje je w czasie, aby uzyskać kąt nachylenia. Wykorzystuje również niewielką część odczytów akcelerometru. Filtr komplementarny minimalizuje w rzeczywistości szum akcelerometru o wysokiej częstotliwości i szum o niskiej częstotliwości żyroskopu, a następnie łączy je w celu uzyskania najlepszego dokładnego kąta nachylenia.

Krok 4: Projekt robota

Zaprojektowaliśmy robota samobalansującego z wykorzystaniem sterownika Proportional Derivative zaimplementowanego przez filtr komplementarny dla MPU6050. Ten mały model robota samobalansującego zilustruje nam przydatność systemów sterowania w samobalansowaniu robotów.

Implementacja systemu:

System jest robotem samobalansującym. Jest on realizowany za pomocą regulatora PID, który jest regulatorem proporcjonalno-całkująco-pochodnym. Równoważymy robota, jadąc jego kołami w kierunku jego upadku. Robiąc to, staramy się utrzymać środek ciężkości robota nad punktem obrotu. Aby jechać kołami w kierunku, w którym spada, powinniśmy wiedzieć, gdzie spada robot i z jaką prędkością spada. Dane te są uzyskiwane za pomocą MPU6050, który ma akcelerometr i żyroskop. MPU6050 mierzy kąt nachylenia i przekazuje dane wyjściowe do mikrokontrolera. MPU6050 jest połączony z płytą STM przez I2C. W I2C jeden przewód służy do zegara o nazwie SCL. Drugi służy do przesyłania danych, czyli SDA. W tym przypadku wykorzystywana jest komunikacja master-slave. Adres początkowy i adres końcowy określa się, aby wiedzieć, skąd dane się zaczynają i gdzie się kończą. Zaimplementowaliśmy tutaj filtr komplementarny dla MPU6050, który jest filtrem matematycznym łączącym wyjścia akcelerometru i żyroskopu. Po uzyskaniu danych z MPU6050 mikrokontroler wykona obliczenia, aby wiedzieć, gdzie spada. Na podstawie obliczeń mikrokontroler STM będzie wydawał polecenia kierowcy silnika, aby kierował pojazdami w kierunku opadania, co zrównoważy robota.

Krok 5: Komponenty projektu

W projekcie robota samobalansującego zastosowano następujące komponenty:

STM32F407

Mikrokontroler zaprojektowany przez ST Microelectronics. Działa na architekturze ARM Cortex-M.

Sterownik silnika L298N

Ten układ scalony służy do uruchamiania silnika. Otrzymuje dwa zewnętrzne wejścia. Jeden z mikrokontrolera, który dostarcza mu sygnał PWM. Regulując szerokość impulsu, można regulować prędkość silnika. Drugim wejściem jest źródło napięcia potrzebne do napędzania silnika, którym w naszym przypadku jest akumulator 12V.

Silnik prądu stałego

Silnik prądu stałego pracuje na zasilaniu prądem stałym. W tym eksperymencie silnik prądu stałego pracuje przy użyciu transoptorów podłączonych do sterownika silnika. Do napędu silnika wykorzystaliśmy Motor Drive L298N.

MPU6050

MPU6050 służy do uzyskania informacji o tym, gdzie spada robot. Mierzy kąt nachylenia w stosunku do zerowego punktu nachylenia, który jest pozycją MPU6050 w momencie uruchomienia programu.

MPU6050 posiada 3-osiowy akcelerometr i 3-osiowy żyroskop. Akcelerometr mierzy przyspieszenie wzdłuż trzech osi, a żyroskop mierzy prędkość kątową wokół trzech osi. Aby połączyć dane wyjściowe, musimy odfiltrować odgłosy obu. Aby odfiltrować szumy, mamy filtr Kalmana i komplementarny. W naszym projekcie wdrożyliśmy filtr komplementarny.

Para optoelektroniczna 4N35

Transoptor to urządzenie służące do izolowania części niskonapięciowej i części wysokonapięciowej obwodu. Jak sama nazwa wskazuje, działa w oparciu o światło. Gdy część niskonapięciowa otrzymuje sygnał, prąd płynie w części wysokonapięciowej

Krok 6: Struktura robota

Struktura robota jest wyjaśniona w następujący sposób:

Struktura fizyczna

Samobalansujący robot składa się z dwóch warstw wykonanych z przezroczystego, plastikowego szkła. Szczegóły dwóch warstw podano poniżej:

Pierwsza warstwa

W dolnej części pierwszej warstwy umieściliśmy ogniwo do zasilania płytki STM. Po każdej stronie umieszczono również dwa silniki o napięciu 4 V każdy z podłączonymi oponami, aby robot mógł się poruszać. W górnej części pierwszej warstwy umieszczono dwa akumulatory 4 V każdy (łącznie 8 V) oraz sterownik silnika IC(L298N) do obsługi silników.

Druga warstwa

W górnej warstwie robota umieściliśmy płytkę STM na płycie perforowanej. Kolejna płyta perforowana z 4 łącznikami optycznymi jest umieszczona na górnej warstwie. Żyroskop jest również umieszczany na górnej warstwie robota od dołu. Oba elementy są umieszczone w środkowej części, tak aby środek ciężkości był jak najniżej.

Środek ciężkości robota

Środek ciężkości jest utrzymywany jak najniżej. W tym celu umieściliśmy ciężkie akumulatory na dolnej warstwie, a lekkie elementy, takie jak płyta STM i transoptory na górnej warstwie.

Krok 7: Kod

Kod został skompilowany na Atollic TrueStudio. Studio STM zostało użyte do debugowania.

Krok 8: Wniosek

Po wielu eksperymentach i obserwacjach dochodzimy w końcu do punktu, w którym podsumowujemy nasze wyniki i dyskutujemy, jak daleko udało nam się wdrożyć i wypracować skuteczność systemu.

Przegląd ogólny

Podczas eksperymentu prędkość silnika była z powodzeniem kontrolowana za pomocą algorytmu PID. Krzywa jednak nie jest dokładnie gładką linią prostą. Powodów jest wiele:

• Czujnik, chociaż podłączony do filtra dolnoprzepustowego, nadal zapewnia pewne skończone odbicia; wynika to z nieliniowych oporów i pewnych nieuniknionych przyczyn elektroniki analogowej.

• Silnik nie obraca się płynnie pod niskim napięciem lub PWM. Dostarcza szarpnięć, które mogą spowodować podanie do systemu błędnych wartości.

• Z powodu chybotania czujnik może przeoczyć niektóre szczeliny zapewniające wyższe wartości. • Inną ważną przyczyną błędów może być częstotliwość taktowania rdzenia mikrokontrolera STM. Ten model mikrokontrolera STM zapewnia taktowanie rdzenia 168 MHz. Chociaż rozwiązano ten problem w tym projekcie, istnieje ogólne przekonanie o tym modelu, że nie zapewnia on tak wysokiej częstotliwości.

Prędkość otwartej pętli zapewnia bardzo płynną linię z kilkoma nieoczekiwanymi wartościami. Algorytm PID działa również dobrze, zapewniając bardzo krótki czas ustalania się silnika. Algorytm PID silnika został przetestowany pod różnymi napięciami, utrzymując stałą prędkość odniesienia. Zmiana napięcia nie zmienia prędkości silnika, pokazując, że algorytm PID działa prawidłowo

Skuteczność

Tutaj omawiamy skuteczność regulatora PID, który zaobserwowaliśmy podczas eksperymentu.

Prosta implementacja

Widzieliśmy w części dotyczącej eksperymentów i obserwacji, że regulator PID jest bardzo łatwy do zaimplementowania. Wymaga tylko trzech parametrów lub stałych, które należy ustawić, aby mieć system kontroli prędkości

Niezrównana wydajność dla systemów liniowych

Liniowy regulator PID jest najbardziej wydajny z rodziny regulatorów, ponieważ logika jest bardzo prosta, a zastosowanie jest szeroko rozpowszechnione w przypadku aplikacji liniowych lub dość liniowych.

Ograniczenia

Wyjaśniliśmy w streszczeniu ograniczenia tego systemu. Tutaj omawiamy kilka z nich, które zaobserwowaliśmy.

Wybór stałych

Widzieliśmy, że chociaż regulator PID jest łatwy do zaimplementowania, nadal główną wadą systemu jest to, że etap wyboru wartości stałych jest pracochłonny; bo trzeba dokonywać trudnych obliczeń. Innym sposobem jest metoda trafień i prób, ale to również nie jest skuteczne.

Stałe nie zawsze są stałe

Wyniki eksperymentalne wykazały, że przy różnych wartościach prędkości odniesienia dla silnika regulator PID działał nieprawidłowo przy tych samych wartościach stałych PID. Dla różnych prędkości stałe musiały być wybierane inaczej, co wykładniczo zwiększa koszt obliczeniowy.

Nieliniowe

Zastosowany w naszym przypadku regulator PID jest liniowy, dlatego można go zastosować tylko do układów liniowych. W przypadku systemów nieliniowych sterownik musi być zaimplementowany inaczej. Chociaż dostępne są różne nieliniowe metody PID, wymagają one doboru większej liczby parametrów. To znowu sprawia, że system jest niepożądany z powodu wysokich kosztów obliczeniowych.

Wymagane wstępne naciśnięcie

Pokazaliśmy w części eksperymentalnej, że dla dość małej prędkości odniesienia, gdzie błąd jest dość mały na początku, PWM dostarczany przez PID jest tak mały, że nie generuje wymaganego momentu rozruchowego dla silnika. Tak więc silnik w niektórych próbach nie pracuje lub w innych próbach zapewnia duże przeregulowanie i dłuższy czas ustalania.

Krok 9: Specjalne podziękowania

Specjalne podziękowania dla członków mojej grupy, którzy pomogli mi w realizacji tego projektu.

Wkrótce wrzucę link do filmu.

Mam nadzieję, że uznasz to za interesujące.

Tu Tahir Ul Haq z UET podpisuje kontrakt. Pozdrawiam !!!