
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 11:32.
- Ostatnio zmodyfikowany 2025-01-23 15:03.

Cześć! Aby zaspokoić moje zainteresowanie programowaniem i mam nadzieję pomóc zaspokoić twoje, chciałbym pokazać przeglądarkę 3D, którą zakodowałem w javascript. Jeśli chcesz pogłębić swoją wiedzę na temat gier 3D lub nawet stworzyć własną grę 3D, ta prototypowa przeglądarka 3D jest dla Ciebie idealna.
Krok 1: Teoria

Aby zrozumieć teorię tej przeglądarki 3D, możesz po prostu zbadać sposób, w jaki patrzysz na otoczenie (pomaga mieć tylko jedno znaczące źródło światła). Zauważ, że:
- Obiekty znajdujące się dalej od ciebie zajmują mniejszą część twojego pola widzenia.
- Obiekty znajdujące się dalej od źródła światła mają ciemniejszy kolor.
- Gdy powierzchnie stają się bardziej równoległe (mniej prostopadłe) do źródła światła, ich kolor wydaje się ciemniejszy.
Postanowiłem przedstawić pole widzenia kilkoma liniami wychodzącymi z jednego punktu (analogicznie do gałki ocznej). Podobnie jak kolczasta kula, linie muszą być równomiernie rozmieszczone, aby zapewnić równą reprezentację każdej części pola widzenia. Na powyższym obrazku zauważ, jak linie wychodzące z kuli z kolcami stają się bardziej rozstawione, gdy oddalają się od środka kuli. Pomaga to zwizualizować realizację obserwacji 1 przez program, ponieważ gęstość linii zmniejsza się, gdy obiekty oddalają się od punktu środkowego.
Linie są podstawową jednostką widzenia w programie i każda z nich jest odwzorowana na piksel na wyświetlaczu. Kiedy linia przecina obiekt, odpowiadający jej piksel jest kolorowany na podstawie odległości od źródła światła i kąta od źródła światła.
Krok 2: Teoria wdrożenia

Aby uprościć program, źródło światła jest takie samo jak punkt centralny (gałka oczna: punkt, z którego oglądana jest mapa i skąd wychodzą linie). Analogicznie do trzymania światła tuż przy twarzy, eliminuje to cienie i pozwala znacznie łatwiej obliczyć jasność każdego piksela.
Program wykorzystuje również współrzędne sferyczne, z centralnym punktem widzenia na początku. Umożliwia to łatwe generowanie linii (każda z unikalnym teta: kąt poziomy i phi: kąt pionowy) i stanowi podstawę obliczeń. Linie o tym samym teta są mapowane na piksele w tym samym wierszu. Fis odpowiednich kątów zwiększa się w każdym rzędzie pikseli.
Aby uprościć matematykę, mapa 3D składa się z płaszczyzn ze wspólną zmienną (wspólne x, y lub z), podczas gdy pozostałe dwie nieczęste zmienne są ograniczone do pewnego zakresu, uzupełniając definicję każdej płaszczyzny.
Aby rozejrzeć się za pomocą myszy, równania programu uwzględniają obrót pionowy i poziomy podczas konwersji między układami współrzędnych sferycznym i xyz. Ma to wpływ na wykonanie rotacji na zestawie linii wzroku „kolczastym kuli”.
Krok 3: Matematyka
Poniższe równania umożliwiają programowi określenie, które linie przecinają każdy obiekt, oraz informacje o każdym przecięciu. Wyprowadziłem te równania z podstawowych równań współrzędnych sferycznych oraz równań obrotu 2D:
r=odległość, t=theta(kąt poziomy), p=phi(kąt pionowy), A=obrót wokół osi Y(obrót pionowy), B=obrót wokół osi Z(obrót poziomy)
Kx=(sin(p)*cos(t)*cos(A)+cos(p)*sin(A))*cos(B)-sin(p)*sin(t)*sin(B)
Ky=(sin(p)*cos(t)*cos(A)+cos(p)*sin(A))*sin(B)+sin(p)*sin(t)*cos(B)
Kz=-sin(p)*cos(t)*sin(A)+cos(p)*cos(A)
x=r*Kx
y=r*Ky
z=r*Kz
r^2=x^2+y^2+z^2
oświetlenie=Klight/r*(Kx lub Ky lub Kz)
p=arccos((x*sin(A)*cos(B)+y*sin(A)*sin(B)+z*cos(A))/r)
t=arccos((x*cos(B)+y*sin(B)-p*sin(A)*cos(p))/(r*cos(A)*sin(p)))
Krok 4: Program

Mam nadzieję, że ta prototypowa przeglądarka 3D pomogła Wam zrozumieć działanie wirtualnej rzeczywistości 3D. Po kilku udoskonaleniach i kodowaniu ta przeglądarka z pewnością ma potencjał do wykorzystania w tworzeniu gier 3D.
Zalecana:
ESP32 COVID19 PRZEGLĄDARKA STANU: 4 kroki

ESP32 COVID19 STATUS VIEWER: Ten projekt po prostu uzyskuje status COCID19 w formacie json i wyświetla go w OLED
Przeglądarka i konwerter negatywów filmowych: 8 kroków (ze zdjęciami)

Przeglądarka i konwerter negatywów filmowych: Odnalazłem natychmiastową potrzebę szybkiego przeglądania i nagrywania starych negatywów filmowych. Miałem kilkaset do przejrzenia… Zdaję sobie sprawę, że są różne aplikacje na mój smartfon, ale nie mogłem uzyskać satysfakcjonujących wyników, więc to właśnie zrobiłem
Przeglądarka internetowa Augmented Reality: 9 kroków
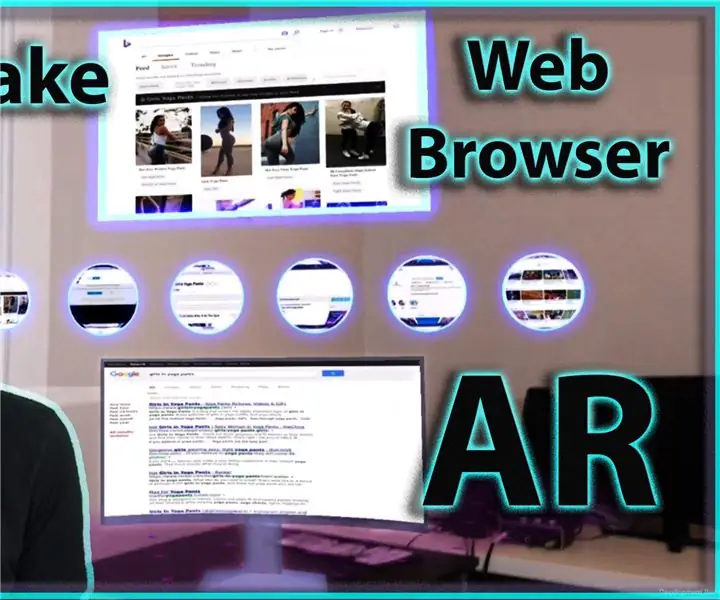
Przeglądarka internetowa Augmented Reality: Dzisiaj zajmiemy się tworzeniem przeglądarki internetowej Augmented Reality dla systemu Android. Ten pomysł zaczął się, gdy ExpressVPN poprosił mnie o zrobienie sponsorowanego filmu na YouTube. Ponieważ jest to mój pierwszy, chciałem zrobić coś, co byłoby istotne dla ich produktu. Pr
Arduino Baby Monitor z przeglądarką Java: 8 kroków (ze zdjęciami)
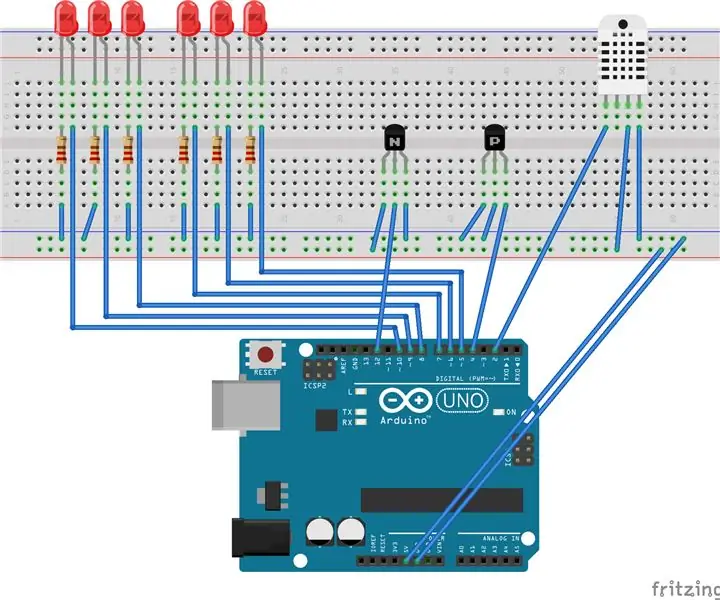
Arduino Baby Monitor z przeglądarką Java: Zbuduj jednostkę wieloczujnikową opartą na Arduino, aby obserwować warunki w pomieszczeniu. To urządzenie może wykrywać wilgotność, temperaturę, ruch i dźwięk. Dołączona jest przeglądarka oparta na javie, która odbiera dane szeregowe z arduino
Przeglądarka zdjęć rentgenowskich na ekranie komputera: 4 kroki
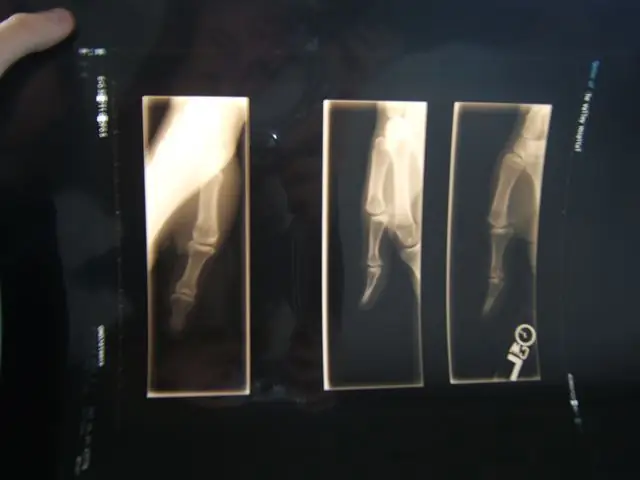
Przeglądarka zdjęć rentgenowskich na ekranie komputera: Jest to prosta metoda korzystania z komputera jako podświetlanej skrzynki do oglądania zdjęć rentgenowskich. Łamanie kości właśnie osiągnęło nowy poziom zabawy
