Rozwiązywanie tabel prawdy: 10 kroków

2024 Autor: John Day | [email protected]. Ostatnio zmodyfikowany: 2024-01-30 11:28

Tabela prawdy to sposób na wizualizację wszystkich skutków problemu. Ten zestaw instrukcji jest przeznaczony dla osób rozpoczynających naukę matematyki dyskretnej. Będziemy ćwiczyć dzisiaj z przykładowym problemem, który jest specyficzny dla tych instrukcji. Do wizualizacji stołu będziesz potrzebować karteczki do zdrapek i ołówka. Ten problem powinien zająć około 5 minut dla osób z wcześniejszą wiedzą na ten temat i około 10 minut dla początkujących.

Dla tego zestawu instrukcji skupimy się na problemie ~p Λ q. Używamy tego do wprowadzenia symboli potrzebnych do interpretacji tablic prawdy.

Krok 1: Zrozumienie tablic prawdy

Tabela prawdy to sposób na wizualizację wszystkich możliwości problemu. Znajomość tablic prawdy jest podstawową potrzebą matematyki dyskretnej. Tutaj znajdziemy wszystkie wyniki dla prostego równania ~p Λ q.

Krok 2: Znajomość symboli

Pierwszym krokiem do tabeli prawdy jest zrozumienie znaków. „~” w tym konkretnym problemie oznacza negację. „p” i „q” to obie zmienne. „Λ” jest równoważne „i”. To równanie jest odczytywane jako „nie p i q”, co oznacza, że równanie jest prawdziwe, jeśli p nie jest prawdziwe i q jest prawdziwe.

Krok 3: Formatowanie tabeli

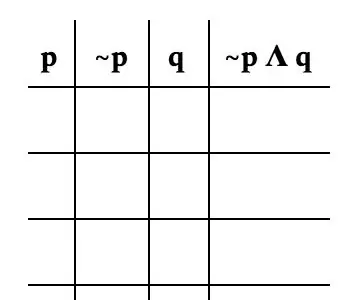
Teraz uformuj rzeczywistą tabelę. Ważne jest, aby rozbić problem według każdej zmiennej. Dla tego problemu podzielimy go następująco: p, ~p, q i ~p Λ q. Obraz jest dobrym przykładem tego, jak powinien wyglądać Twój stół.

Krok 4: Przypisywanie prawdy i fałszu

Ponieważ istnieją tylko dwie zmienne, będą tylko cztery możliwości na zmienną. Dla p dzielimy to na połowę przestrzeni zajmowanych przez T (dla prawdy) i drugą połowę przez F (dla fałszu).

Krok 5: Negacja

Dla ~p piszesz przeciwny znak, który ma p, ponieważ ~p jest przeciwieństwem p.

Krok 6: Zmienna „q”

Dla q naprzemiennie T i F, aby uzyskać każdą możliwą kombinację. Ponieważ równanie skupia się tylko na ~p, możemy zignorować kolumnę p podczas określania prawdziwości równania. Symbol „Λ” oznacza, że zarówno ~p, jak i q muszą być prawdziwe, aby równanie było prawdziwe.

Krok 7: Rozwiązywanie problemu fałszu w ostatniej kolumnie

Dla pierwszego wiersza, ponieważ ~p to F, a q to T, ~p Λ q to F w scenariuszu, w którym ~p to F, a q to T. Jedyny scenariusz, w którym równanie to T, to gdzie ~p to T, a q to T.

Krok 8: Znalezienie prawdy w ostatniej kolumnie

Oznacza to, że jedynym wierszem, który ma T, jest trzeci.

Krok 9: Wykończenie stołu

Dokładnie sprawdź, czy Twój stół jest poprawny. Robisz to, sprawdzając, czy twoje znaki są prawidłowe i upewniając się, że ostatnia kolumna jest wykonana poprawnie. Ostatnia kolumna jest wynikiem wszystkich możliwych permutacji zmiennych.

Krok 10: Gotowe

Teraz, gdy wiesz, jak wykonać podstawową tabelę prawdy, ćwicz dalej! Im więcej ćwiczysz, tym lepiej je wykonujesz.