
Spisu treści:
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 11:29.
- Ostatnio zmodyfikowany 2025-01-23 15:03.
By arrowlikeŚledź Więcej autora:


W klasie często używamy stopera do przeprowadzenia eksperymentu z wahadłem lub prostego eksperymentu z ruchem harmonicznym. Oto wyzwanie, czy możemy stworzyć prawdziwy wykres jego ruchu i zobaczyć, jaka jest chwilowa pozycja kątowa i prędkość, to o wiele więcej informacji i zabawy.
Pierwsze pytanie, musimy zdecydować, że korpus wahadła jest nieważkim sznurem lub sztywnym, jednolitym prętem. Podejście ze sznurkiem wydaje się łatwiejsze. Z praktyki budowania jednego, mam następujące rozważania na temat kompromisu: Najłatwiejszym sposobem zawieszenia systemu wahadłowego może być powieszenie go na górnej krawędzi drzwi. Daje to długość wahadła ~2m bez wykonywania jakichkolwiek prac budowlanych. Ale potrzebuje, aby huśtawka nie dotykała powierzchni drzwi, co po prostu rujnuje cały eksperyment. Tak więc samolot, którym się obraca, powinien być dokładnie równoległy do powierzchni ściany/drzwi. Nieważka linka jest zwykle cienka, łatwo się obraca i komplikuje pomiar kąta wychylenia. Chcemy użyć jednego pomiaru do reprezentowania stanu swingu. Cienki sznur, taki jak żyłka, może być elastyczny i rozciągliwy, co wpływa na jedną z naszych najważniejszych stałych mierzonych przez nas i używanych w równaniu, czyli długość wahadła. Na niektóre może mieć również wpływ temperatura. Ciężarek zawieszony na końcu linki musi być na tyle ciężki, aby ciężar linki stał się znikomy. Proszę o komentarz, jeśli zgadzasz się lub nie zgadzasz z nimi, lub masz inne pomysły na kompromisy projektowe. Do zbadania tego problemu potrzebujemy urządzenia tak lekkiego, że jego wagę można pominąć, a system wahadła nadal traktujemy jak sztywny jednorodny pręt. Używam elektronicznego kontrolera COTS do noszenia, który dostarcza nam informacje o żyroskopie, akcelerometrze i kącie za pośrednictwem połączenia Bluetooth. Te pomiary zostaną zapisane w pliku danych aplikacji telefonu komórkowego. Następnie przeanalizujemy dane dla naszego prostego eksperymentu ruchu harmonicznego. Analiza numeryczna skupia się na następujących tematach: 1) Przewiduj okres drgań wahadła 2) Programowo zbieraj dane z eksperymentu ruchu wahadła prostej harmonicznej 3) Użyj kmean do pogrupowania danych i usunięcia wartości odstających w procesie analizy 4) Użyj krótkiej FFT do oszacowania częstotliwość drgań wahadła
Kieszonkowe dzieci
Aparatura pomiarowa Bluetooth
Aplikacja na telefon z systemem Android: Przejdź do sklepu Google Play, wyszukaj M2ROBOTS i zainstaluj aplikację kontrolną. Jeśli trudno jest uzyskać dostęp do sklepu Google Play, odwiedź moją osobistą stronę główną, aby uzyskać alternatywną metodę pobierania aplikacji
pręt drewniany
kilka części drukowanych w 3D
brzeszczoty lub podobny materiał metalowy
Krok 1: Co to jest wahadło? Jak to modelować?
Istnieje wiele artykułów i książek wprowadzających do wyprowadzania równań wahadła, w tym podręcznik do nauki fizyki. Takich treści lepiej nie powtarzać tutaj ponownie. Przytaczam tu jedynie końcowy wniosek dotyczący "prostego ruchu harmonicznego". Aby poznać okres wahadła, wystarczy znać długość wahadła, oznaczoną jako „l”, w metrach.
Jeśli mamy wystarczającą pewność, że ciężarek znajduje się prawie całkowicie na końcu nieważkości sznura zawieszonego na czopie, a wahadło kołysze się pod małymi kątami θ, powiedzmy mniejszymi niż 15°, okres T1 takiego wahadła jest określony wzorem:
T1 = 2*pi*(l/g)^0,5
g = przyspieszenie grawitacyjne, około 9,8 m/s^2
Jeśli nieważki sznur zostanie zastąpiony sztywnym, jednolitym prętem, ponownie o długości l, jego okres ruchu harmonicznego prostego T2 jest wyrażony jako T1 = 2*pi*(2l/3g)^0,5
W rzeczywistości ma ten sam okres, co nieważkie wahadło sznurkowe, stanowiące dwie trzecie sztywnej, jednolitej długości pręta.
To jest tło i możemy zacząć przygotowywać nasz eksperyment.
Krok 2: Przygotuj części do budowy sprzętu



Aby zbudować strukturę wahadła, drukujemy niektóre części w 3D i poddajemy recyklingowi coś, co już mamy. Ogólną strukturę wahadła pokazano na rys.1. Jest to mieszanka części do druku 3D wraz z kilkoma ręcznie wykonanymi częściami i długim kawałkiem drewnianego pręta od Lowe's.
Część wydrukowana w 3D na Rys. 2 jest zawieszona na górnej krawędzi drzwi, ponieważ nasze drzwi są łatwą, płaską powierzchnią, na której możemy coś powiesić. Link do pobrania pliku STL:
xiapeiqing.github.io/doc/kits/pendulum/pen…
Zielona część na Rys. 3 łączy drewniany pręt z ostrzem, a ostrze znajduje się na szczycie dwóch kawałków szyny zamontowanych na wcześniejszym wydrukowanym w 3D wieszaku na drzwi. Link do pobrania pliku STL:
Dwa kawałki szyny są wykonane przez przełamanie starego brzeszczotu na pół, patrz rys. 4. Część na rys. 2 przygotowała dla nich odpowiedni rozmiar szczeliny. Idealnie możemy wykonać nacięcie w kształcie litery "V" w tych dwóch brzeszczotach za pomocą pilnika. Metal o dość ostrych krawędziach, taki jak jednoostrzowa żyletka lub dowolny ręcznie wykonany metalowy element, może znajdować się wewnątrz nacięć w kształcie litery „V”. Powodem, dla którego potrzebujemy mniejszej powierzchni kontaktu, jest zmniejszenie energii kinetycznej traconej podczas kołysania.
Ostatnia wydrukowana w 3D część na ryc. 5 to mała tacka do przechowywania elektronicznego aparatu pomiarowego.
Link do pobrania:
Urządzenie pomiarowe bluetooth generuje oszacowanie kąta, pomiar żyroskopowy i pomiar akcelerometru. Wszystkie te dane są dla nas dostępne za pośrednictwem bezprzewodowego łącza bluetooth.
Przeprowadzimy wiele eksperymentów, umieszczając ten aparat w różnych pozycjach ramienia wahadła i zobaczymy różnice.
Krok 3: Zbieranie danych eksperymentu



Istnieją dwie wykonalne metody zbierania danych eksperymentalnych przed analizą zebranego zbioru danych:
1) Użyj aplikacji na telefon z systemem Android określonej w sekcji wymagań, aby zarejestrować wszystkie pomiary wykonane przez urządzenie w pliku danych przechowywanym na karcie SD telefonu. Możemy skopiować plik i przetworzyć informacje.
2) Użyj komputera z obsługą Bluetooth, PC, laptopa lub minikomputera RaspberryPi, aby nawiązać połączenie Bluetooth z urządzeniem i odczytać dane do analizy w czasie rzeczywistym lub offline.
Istnieją zarówno zalety, jak i wady dla każdej metody, spróbujemy obu i odróżnimy tę instrukcję.
W przypadku metody (1) przy użyciu aplikacji na Androida, po przejściu do interfejsu sterowania aplikacji na Androida, dane telemetryczne wysłane z urządzenia pomiarowego Bluetooth do telefonu z systemem Android zostaną zapisane w pliku dziennika danych o nazwie m2flightDatayyyymmdd_hhmmss.txt. Można go znaleźć w folderze Download/m2LogFiles telefonu z Androidem. Folder „Pobierz” to wcześniej istniejący folder w systemie Android telefonu, a „m2LogFiles” to folder utworzony przez aplikację. Treść nazwy pliku rrrrmmdd_ggmmss to sposób na zakodowanie czasu rozpoczęcia eksperymentu (rok, miesiąc, dzień, godzina, minuta i sekunda) w nazwie pliku.
Każdy wiersz w pliku dziennika to jeden rekord. Rozpoczyna się sygnaturą czasową zdarzenia, ciągiem preambuły „eam:”, po którym następują 4 dane trypletowe, którymi są:
Odczyt osi XYZ akcelerometru w surowych wartościach odczytu rejestru sprzętowego czujnika
Odczyt osi XYZ żyroskopu w surowych wartościach odczytu rejestru sprzętowego czujnika
Odczyt osi XYZ magnetometru w surowych wartościach odczytu rejestru sprzętowego czujnika
szacowany na pokładzie Roll/Pitch/Surowy w stopniach
Plik danych utworzony za pomocą programu komputerowego Python będzie używał identycznego formatu pliku danych, dzięki czemu program, którego używamy w kroku analizy danych, nie będzie przeszkadzał w źródle danych generowanym przez nasz program Python lub aplikację na Androida.
Zacznijmy kodować od metody (2).
Do interakcji z urządzeniem pomiarowym bluetooth dostępne są dwie wersje SDK:
1) Python SDK, który można zainstalować za pomocą „pip3 install m2controller”, używanym językiem jest python3. Przykładowy kod aplikacji użytkownika jest przechowywany w https://github.com/xiapeiqing/m2robots/tree/maste… Do tego eksperymentu użyjemy skryptu Pythona pendulum1.py
2) Java SDK, który nie jest używany w tej instrukcji, ponieważ chcemy później wizualizować i analizować nabyte dane wahadła, co może wymagać trochę więcej wysiłku, abyśmy mogli zaprogramować w Javie.
Kod źródłowy programu python3 do zbierania danych zawiera wiele komentarzy dotyczących szczegółów funkcji kodu. Tutaj znajduje się migawka kodu źródłowego.
#!/usr/bin/env python# -*- kodowanie: UTF-8 -*- z m2controller import m2controller z m2controller import m2Const import sygnału import czas import datetime import usrCfg import pendulum2
requestExit = Fałsz
################################################################
# chcemy użyć tej samej konwencji nazewnictwa plików dziennika, aby moduł analizy danych, pendulum2.py, mógł być niezależny od sposobu, w jaki otrzymujemy plik danych dziennika ################# ############################################### logfilename = " m2flightData%s.txt"%(datetime.datetime.fromtimestamp(time.time()).strftime('%Y%m%d_%H%M%S')) dataLogfile = open(logfilename, "w")
def signal_handler(sig, ramka):
global requestExit print('użytkownik Ctrl-C, aby zakończyć wykonywanie programu') requestExit = True signal.signal(signal. SIGINT, signal_handler)
################################################################
# po każdym udostępnieniu danych pomiarowych z częstotliwością 20Hz ta funkcja "oddzwaniania" zostanie przywołana ################################# ################################### def callbackfunc(telemetria): strTimeStamp = datetime.datetime.fromtimestamp(time.time ()).strftime('%H:%M:%S.%f')[:-3] dataStr = "%s, eam:%d, %d, %d, %d, %d, %d, %d, %d, %d, %2.1f, %2.1f, %2.1f\n"%(strTimeStamp, telemetria['m_fAccelHwUnit'][0], telemetria['m_fAccelHwUnit'][1], telemetria['m_fAccelHwUnit'][2], telemetria['m_fGyroHwUnit'][0], telemetria['m_fGyroHwUnit'][1], telemetria['m_fGyroHwUnit'][2], telemetria['m_fMagHwUnit'][0], telemetria['m_fMagHwUnit'][1], telemetria['m_fMagHwUnit'][2], telemetria['m_fRPYdeg'][0], telemetria['m_fRPYdeg'][1], telemetria['m_fRPYdeg'][2]) ## ################################################## ############ # wypisujemy ciąg danych na ekran i zapisujemy je do pliku logu ###################### ########################################## print(dataStr) dataLogfile.writelines(DataStr)
################################################################
# zainicjuj kontroler pamiętaj, aby w polu BleMACaddress ustawić adres MAC Twojego urządzenia ################################# ############################### # DO ZROBIENIA: zainicjujmy adres BleMACaddress, jeśli nie został ustawiony przez użytkownika. controller = m2controller. BleCtrller(m2Const.etDebian, callbackfunc, usrCfg. BleMACaddress) controller.connect() podczas True: ########################## ######################################## # czekaj na dane pomiarowe utworzone i wysłane z pomiaru wahadłowego aparatura ################################################### ############### controller.m_CommsTunnel.waitForNotifications(1.0) jeśli requestExit: ######################## ########################################## # prowadzenie domu działa tutaj, gdy zakończymy rejestrację danych ################################################## ############## controller.stop() dataLogfile.close() przerwa
################################################################
# zbieranie danych zakończone, teraz przeanalizujmy dane logu ####################################### ######################### pendulum2.parseDataLogFile(logfilename)
Aby uzyskać długoterminową aktualizację, przejdź do kasy
Teraz wyjaśnijmy jego sposób działania. Ten program Pythona jest napisany na wierzchu pakietu instalacyjnego pip o nazwie m2controller. Pakiet niższego poziomu oferuje mechanizm wywołań zwrotnych, dzięki czemu każda odebrana aktualizacja pomiaru wyzwoli napisaną przez nas funkcję wywołania zwrotnego i zapisze dane w lokalnym pliku logu. Format zawartości danych pliku dziennika jest identyczny z formatem tworzonym przez aplikację towarzyszącą na Androida, dzięki czemu plik dziennika danych utworzony przez program python lub aplikację towarzyszącą android jest wymienny.
Sygnał ctrl-C użytkownika, przechwycony przez system operacyjny, jest przekazywany do programu i zatrzymuje nieskończoną pętlę w oczekiwaniu na nowe dane pomiarowe.
Do tej pory plik dziennika został pomyślnie utworzony, a ten program wywoła program analityczny w celu zbadania wyników naszego eksperymentu.
Oto dwa eksperymenty, a porównanie pokazuje bardzo wyraźną różnicę, dołączając 7-gramowe urządzenie w różnych miejscach.
Na ryc. 2 używamy wagi do określenia rzeczywistej wagi tego urządzenia pomiarowego bluetooth.
Ryc. 3 przedstawia konfigurację wahadła, w której urządzenie o wadze 7 gram jest przymocowane do dolnego końca wahadła. Konfiguracja ustawienia na rys. 4 ma masę 7 gramów umieszczoną znacznie bliżej wahliwej osi.
Ryc. 5 to widok zbliżenia struktury wahadła.
Krok 4: Analiza danych



Urządzenie pomiarowe bluetooth waży ~ 7 gramów, co waży znacznie mniej niż drewniany kij o długości ~ 1,6 metra. Użyj założenia "sztywnego jednolitego pręta" i otrzymamy to równanie okresu wahadła, T1 = 2*pi*(2l/3g)^0,5
Aby uzyskać stałą grawitacji, możemy użyć 9,8m/s^2. Ale dokładniejszą stałą grawitacji w dowolnej geolokalizacji można pobrać z tej usługi internetowej:
www.wolframalpha.com/widgets/view.jsp?id=e…
W przypadku san francisco jest to 9,81278 m/s^2
Długość wahadła mierzona jest na 64,5 ''
2*pi*sqrt(2*64,5*0,0254/(3*9.81278)) daje oczekiwany okres wahadła 2,0962(sek).
Zobaczmy, czy zgadza się to z naszymi eksperymentami.
W pierwszym eksperymencie układ wahadła ma 7-gramowe urządzenie przymocowane do dolnego końca wahadła. Mój plik dziennika można pobrać w:
xiapeiqing.github.io/doc/kits/pendulum/pen…
Zmień jego nazwę na „PendulumTestData.txt” i umieść w tym samym folderze programu do analizy Pythona. Tutaj znajduje się migawka kodu źródłowego.
#!/usr/bin/env python# -*- kodowanie: UTF-8 -*- importuj csv importuj matplotlib.pyplot jako plt plt.style.use('seaborn-whitegrid') importuj numpy jako np z datetime importuj datetime, timedelta import seaborn jako sns z sklearn.cluster import KMeans z kolekcji import licznika ################################### ############################### # ta funkcja uruchamia prace analizy pliku danych ############ ################################################## ## def parseDataLogFile(nazwaplikudanych): ########################################## ###################### # wyodrębnij dane w pliku dziennika danych oddzielonych przecinkami (CSV) i zapisz zawartość każdej kolumny w jednej zmiennej typu float ## ################################################## ############ z open(datafilename) jako csvfile: readCSV = csv.reader(csvfile, delimiter=', ') timestampS = fAccelHwUnit_x = fAccelHwUnit_y = fAccelHwUnit_z = fGyroHwUnit_x = fGyroHwUnit_y = fGyroHwUnit_z = fMagHwUnit_x = fMagHwUnit_y = fMagHwUnit t_z = fRPYdeg_r = fRPYdeg_p = fRPYdeg_y = dla wiersza w readCSV: try: x = datetime.strptime(row[0].split(', ')[0], '%H:%M:%S.%f') znacznik czasuS.append(timedelta(godziny=x.godzina, minuty=x.minuta, sekundy=x.sekunda, mikrosekundy=x.mikrosekunda).total_seconds()) fAccelHwUnit_x.append(float(wiersz [1][4:])) fAccelHwUnit_y.append(float(wiersz[2])) fAccelHwUnit_z.append(float(wiersz[3])) fGyroHwUnit_x.append(float(row[4])) fGyroHwUnit_y.append(float (row[5])) fGyroHwUnit_z.append(float(row[6])) fMagHwUnit_x.append(float(row[7])) fMagHwUnit_y.append(float(row[8])) fMagHwUnit_z.append(float(row [9])) fRPYdeg_r.append(float(row[10])) fRPYdeg_p.append(float(row[11])) fRPYdeg_y.append(float(row[12])) z wyjątkiem: pass timestampS = np.asarray(Znaczniki czasowe), znaczniki czasu = znaczniki czasu - Znaczniki czasowe [0] fAccelHwUnit_x = np.asarray (fAccelHwUnit_x) fAccelHwUnit_y = np.asarray (fAccelHwUnit_y) fAccelHwUnit_z = np.asarray (fAccelHwUnit_z) fGyroHwUnit_x = np.asarray (fGyroHwUnit_x) fGyroHwUnit_y = np.asarray (fGyroHwUnit_y) fGyroH wUnit_z = np.asarray (fGyroHwUnit_z) fMagHwUnit_x = np.asarray (fMagHwUnit_x) fMagHwUnit_y = np.asarray (fMagHwUnit_y) fMagHwUnit_z = np.asarray (fMagHwUnit_z) fRPYdeg_r = np.asarray (fRPYdeg_r) fRPYdeg_p = np.asarray (fRPYdeg_p) fRPYdeg_p = fRPYdeg_p - np. średnia (fRPYdeg_p) fRPYdeg_y = np. asarray (fRPYdeg_y)
################################################################
# potrzebujemy dokładnego oszacowania częstotliwości próbkowania dla dokładnego oszacowania okresu oscylacji ###################################### ############################ FsHz = getSamplingIntervalS(timestampS) ################ ################################################ # posługiwać się składowa pochylenia w danych wyjściowych układu odniesienia kursu przestrzennego dla analizy okresu wahadła ####################################### ########################### analysis_timeSequence(timestampS, fRPYdeg_p, FsHz, 'pitch') ########### ################################################## ### # użyj danych wyjściowych surowych pomiarów akcelerometru do analizy okresu wahadła ####################################### ########################### analysis_timeSequence(timestampS, fAccelHwUnit_x, FsHz, 'accel') ########### ################################################## ### # używaj wyjściowych pomiarów surowych żyroskopów do analizy okresu wahadła ####################################### ########################### analysis_timeSequence(timestampS, fGyroHwUnit_y, FsHz, ' żyroskop') print('zrobione, gratulacje:-)') plt.show() ############################### ################################### # w procesie komunikacji bluetooth istnieje rzadka szansa, że pakiet transmisji danych może być zgubionym # używamy średniej K do odizolowania danych pomiarowych 20Hz od wartości odstających, które są spowodowane przez odrzucony pakiet # zanurz się w "sygnał i system po więcej szczegółów" ################ ################################################ def getSamplingIntervalS (sygnatura czasowa): plt.figure() sampleIntervalS = np.diff(timestampS) sns.distplot(sampleIntervalS) plt.ylabel('histogram') plt.xlabel('interwał(y) pomiaru') clusterCnt = 5 km = KMeans(n_clusters = clusterCnt) km.fit(sampleIntervalS.reshape(-1, 1)) centroids = km.cluster_centers_elemCnt = Counter(km.labels_)występowanieCnt = for ii in range(clusterCnt):występowanieCnt.append(elemCnt[ii]) FsHz = 1/centroids[occurrenceCnt.index(max(occurrenceCnt))] return FsHz
################################################################
# użyj spektrometru, tj. krótkiego czasu FFT, aby uzyskać składową częstotliwości, pik bin jest naszym najlepszym oszacowaniem oscylacji wahadła ########################## ######################################## def analysis_timeSequence(timestampS, timeSeqData, FsHz, strComment): fig, (ax1, ax2) = plt.subplots(nrows=2) ax1.plot(timestampS, timeSeqData, marker='o', markerfacecolor='blue', markersize=2, color='skyblue', linewidth=1) ax1.set_title("pomiar w dziedzinie czasu wahadła -- %s"%strComment) ax1.set_xlabel("Czas próbkowania (sekunda)") ax1.set_ylabel(strComment); NFFT = 2048 # długość segmentów okienkowania
Pxx, freqs, bins, im = ax2.specgram(timeSeqData, NFFT=NFFT, Fs=FsHz, noverlap=NFFT/2)
ax2.set_title("Spektrogram") ax2.set_xlabel("próbki") ax2.set_ylabel("częstotliwość(Hz)");
# Metoda `specgram` zwraca 4 obiekty. Oni są:
# - Pxx: periodogram # - freqs: wektor częstotliwości # - bins: środki przedziałów czasu # - im: instancja matplotlib.image. AxesImage reprezentująca dane na wykresie pkresult = np.where(Pxx == np..amax(Pxx)) oscFreqHz = freqs[pkresult[0][0] print('oscylacja wahadła Freq(Hz)=%f, Period(Sec)=%f, źródło danych estymacji: %s'%(oscFreqHz, 1/oscFreqHz, strComment)) powrót 1/oscFreqHz
################################################################
# czy mamy uruchamiać ten program niezależnie, tzn. nie będąc wywoływanym przez pendulum1.py, # definiujemy domyślną nazwę pliku z danymi dziennika do analizy #################### ############################################ jeśli _name_ == "_main_ ": defaultFilename = './PendulumTestData.txt' import os.path if os.path.isfile(defaultFilename): parseDataLogFile(defaultFilename) else: print ("domyślny plik dziennika %s nie istnieje"%defaultFilename)
Aby uzyskać długoterminową aktualizację, przejdź do kasy
Kod źródłowy zawiera szczegółowe komentarze, podajmy tutaj ogólne podsumowanie matematycznego oszacowania.
1) Najpierw odczytujemy zawartość pliku CSV do komputera, używając pakietu Pythona o nazwie „csv”. Prowadzimy pomiary okresowe.
21:34:26,362, eam:0, -128, 14464, -8, 144, -96, 2112, -1280, 1664, -0,5, -5,5, 40,5
21:34:26,373, eam:128, 0, 14272, -8, 136, 40, 2112, -1280, 1664, -0,5, -6,5, 40,0
21:34:26.412, eam:448, -64, 14208, -8, 136, 24, 2176, -1280, 1664, -0.5, -7.5, 40.5
21:34:26,462, eam:448, -128, 14272, -8, 120, 16, 2176, -1280, 1664, -0,5, -8,0, 40,5
2) Ponieważ szybkość pomiaru jest tak krytyczna i bezpośrednio wprowadza błąd estymacji okresu wahadła, chcemy je oszacować. Nasz nominalny interwał pomiarowy to 50ms, czyli 20Hz. Średnia ze wszystkich pomiarów wydaje się OK, ale czasami tracimy pakiet transmisji danych, interwał aktualizacji wynosi 100ms lub 150ms, …
Jeśli wykreślimy występowanie tych danych, patrz ryc. 1, jako człowiek, możemy łatwo uzyskać wartość gałek ocznych 0,05 sekundy. Czy jednak możemy zrobić coś lepszego?
Musimy użyć metody klasyfikacji, aby wybrać tylko te dobre do uśrednienia obliczeń. Python ma zestaw narzędzi o nazwie KMeans, który pomaga nam w klastrowaniu, lub powiedzmy, klasyfikacji. Koncepcje te są wykorzystywane w wielu obszarach Big Data i AI.
3) Rys.2 zawiera dwa obrazy. Górny wykres to sekwencja w dziedzinie czasu naszego pomiaru kąta wychylenia w stopniach. Odwołując się do znacznika czasu osi x w sekundzie, możemy odczytać około 22,5 cykli w ciągu 50 sekund, co przekłada się na okres wahadła 2,22 sekundy. Czy istnieje sposób na zautomatyzowanie tego procesu i dokładniejsze oszacowanie? Tak, możemy użyć narzędzia matematycznego zwanego spektrogramem, które wykorzystuje mały fragment danych pomiarowych i podaje nam częstotliwość, patrz rysunek poniżej. Odczyt na osi y dla najciemniejszej linii to częstotliwość drgań wahadła. Będąc linią poziomą potwierdza, że oscylacja wahadła nie zmieniła się w ogóle podczas eksperymentu. Odwrotną wartością częstotliwości drgań jest okres drgań wahadła.
Raport końcowy sporządzony przez program to podsumowanie tekstowe:
oscylacja wahadła Freq(Hz)=0,449224, Okres(Sek)=2,226059, źródło danych szacunkowych: wysokość tonu
Możemy stwierdzić, że nasz wcześniejszy wynik obliczenia ręki, 2,22 s, jest dość zgodny z wartością obliczoną przez program.
W porównaniu do 2,0962 (s) obliczonej teoretycznie wartości, pozostało ~5% błędu. Jak się ich pozbyć? Pamiętasz założenie "sztywnego jednolitego pręta"? Nawet 7 gramowy dodatkowy ciężar wydaje się banalny, jest to największa przyczyna pozostałego błędu.
Przesuwamy teraz urządzenie blisko osi. Zobacz poprzedni krok, aby zobaczyć zbliżenie. Utworzony przeze mnie plik dziennika można pobrać tutaj:
xiapeiqing.github.io/doc/kits/pendulum/pen…
Uruchom te same kroki analizy i otrzymamy Okres 2,089867 (Sek), patrz Rys. 3, który jest prawie identyczny z przewidywaniem teoretycznym. Świetny!
Ponieważ mamy nie tylko pomiar kąta wychylenia, ale także pomiar żyroskopowy i pomiar akcelerometrem w tym samym tempie. Przeprowadź tę samą analizę dla pozostałych dwóch pomiarów, otrzymamy wyniki na rys. 4 i 5. Szacunki ze wszystkich trzech źródeł pomiarowych są zgodne, co daje nam większą pewność sukcesu naszego eksperymentu.
Oto wynik końcowy działania programu python:
oscylacja wahadła Freq(Hz)=0,478499, Okres(Sek)=2,089867, źródło danych szacunkowych: wysokość tonu
oscylacja wahadła Freq(Hz)=0,478499, Okres(Sec)=2,089867, estymacja źródło danych: accel
oscylacja wahadła Freq(Hz)=0,478499, Okres(Sek)=2,089867, źródło danych szacunkowych: żyroskop
Ostatnia myśl na tym etapie, w jaki sposób wyniki estymacji mogą być dokładnie identyczne przy użyciu różnych źródeł danych wejściowych? To jest kontr-intuicja. To pytanie pozostawiam czytelnikom. Oto wskazówka: pamiętasz, że do oszacowania częstotliwości drgań używamy krótkoczasowej FFT? W dziedzinie cyfrowej estymata częstotliwości jest podawana w dyskretnych przedziałach częstotliwości zamiast estymacji liczby zmiennoprzecinkowej.
Krok 5: Zalecenia dotyczące przyszłej pracy
Istnieje kilka kategorii zaleceń dotyczących przyszłej pracy.
Na wcześniejszym etapie udało nam się zmniejszyć błąd eksperymentu z ~5% do mniej niż 1%, czy możemy zrobić coś lepszego? Zauważając, że wielkość oscylacji zmniejsza się wykładniczo, jednym z czynników może być opór powietrza spowodowany kołysaniem wahadła. Przekrój poprzeczny wahadła może wymagać modyfikacji, aby uzyskać opływowy kształt, aby zmniejszyć opór aerodynamiczny.
Czy możemy zastosować zmienne w czasie wzmocnienie wyuczone za pomocą technik filtrów adaptacyjnych, aby wyprowadzić sygnał o stałej wartości szczytowej? W międzyczasie skoreluj wielkość tłumienia z siłami zewnętrznymi.
Trudno znaleźć coś prostszego niż „prosty ruch harmoniczny”. Czy możemy użyć urządzeń, w których analizujemy wahadło, aby przeanalizować coś bardziej skomplikowanego, aktywność sportową, sekwencję startu rakiety wodnej itp.?
Miłego hackowania
Zalecana:
Tworzenie prostego robota z rzeczy, które możesz znaleźć w swoim domu (wersja hotwheel): 5 kroków

Tworzenie prostego robota z rzeczy, które możesz znaleźć w swoim domu (wersja hotwheel): Ten instruktaż pokaże ci, jak zrobić hotwheel, który działa sam i działa na bateriach podwójnego A. Będziesz musiał używać tylko rzeczy, które najprawdopodobniej znajdziesz w swoim domu. Należy pamiętać, że ten robot prawdopodobnie nie będzie szedł dokładnie prosto, a
Badanie recepty na gałkę oczną: projekt BME60B: 9 kroków

Okiem na receptę gałki ocznej: projekt BME60B: Autor: Hannah Silos, Sang Hee Kim, Thomas Vazquez, Patrick VistePowiększenie jest jedną z kluczowych cech okularów do czytania, które są klasyfikowane według ich recepty na dioptrie. Według Michigan Technology University, dioptrii to fo
Badanie symulacyjne: 9 kroków
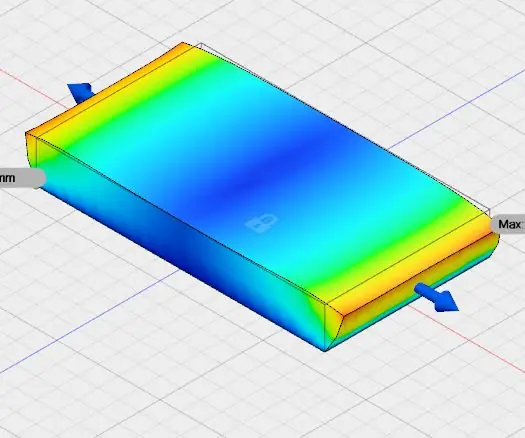
Badanie symulacyjne: W tej instrukcji użyłem fusion 360 firmy Autodesk. Ta instrukcja dotyczy badania symulacyjnego. W tym wykorzystałem obszar roboczy modelu i symulacji automatycznego fuzji biurek 360. Przestudiowałem symulację sił wzdłużnych o wartości 10 N
Badanie pyłu Arduino: 8 kroków

Arduino Dust Study: Jak wyglądałoby życie na Marsie? Czy powietrze nadaje się do oddychania? Czy to bezpieczne? Ile tam jest kurzu? Jak częste są burze? Czy kiedykolwiek zastanawiałeś się, jaka jest odpowiedź na którekolwiek z tych pytań?
Badanie efektu struktury rezonansowej za pomocą papierowego plastra miodu: 6 kroków

Badanie efektu struktury rezonansowej za pomocą papierowego plastra miodu: Pomyślałem, że ci, którzy lubią interesować się alternatywnymi tematami energii, mogą spróbować tego. Opiera się na odkryciu Wiktora Grebennkowa. Historię można znaleźć w wielu miejscach, ale ta na keelynet była tą, którą znalazłem http://www.keelynet.com/gr
