Badanie recepty na gałkę oczną: projekt BME60B: 9 kroków

2024 Autor: John Day | [email protected]. Ostatnio zmodyfikowany: 2024-01-30 11:27

Autor: Hannah Silos, Sang Hee Kim, Thomas Vazquez, Patrick Viste

Powiększenie jest jedną z kluczowych cech okularów do czytania, które są klasyfikowane według korekcji dioptrii. Według Michigan Technology University, dioptrie to ogniskowa obiektywu, zwykle mierzona w mm, w metrach (Michigan Technology University). Ponieważ okulary do czytania mają soczewki wypukłe, ogniskowa byłaby dodatnia, powodując, że dioptrie również byłyby dodatnie (HyperPhysics). Ogniskowa zwiększa się, gdy odległość między obiektem oddala się od rzeczywistej soczewki, a to prowadzi do zmniejszenia dioptrii, ponieważ są one odwrotnie proporcjonalne. Dlatego posiadanie okularów do czytania z dodatkowymi dioptriami pomogłoby obiektywowi powiększyć widok tak, że może wydawać się, że ogniskowa jest mniejsza poprzez zwiększenie wartości dioptrii.

Przedstawiony kod posłuży do przewidzenia dioptrii soczewki o nieznanej recepcie. Do obliczenia recepty wykorzystuje się dwa dane wejściowe: zdjęcie kontrolowanego tła bez użycia jakichkolwiek soczewek i inną fotografię tego samego tła, ale przez wybrany obiektyw. Program zmierzy dystorsję między tymi dwoma zdjęciami. Stamtąd będziemy mogli oszacować dioptrię obiektywu i uzyskać wynik, który zobaczy użytkownik.

Do tego Instruktażowego będziesz potrzebować:

• Czarno-biały wzór szachownicy wydrukowany na kartce papieru o wymiarach 11x8,5
• Aparat z możliwością zablokowania ostrości
• Statyw lub coś podobnego do zabezpieczenia aparatu
• Różne recepty okularów do czytania
• MATLAB

Krok 1: Rób zdjęcia

Aby obliczyć powiększenie obiektywu, musisz być w stanie porównać je z rzeczywistym rozmiarem obiektu. W tym projekcie będziemy porównywać powiększony obraz z obrazem kontrolnym.

Tak więc pierwszym krokiem jest zrobienie dwóch zdjęć tego samego obrazu - pierwszego przez sam aparat, a drugiego przez obiektyw okularów do czytania, które chcesz przetestować.

Zrobisz zdjęcie czarno-białej szachownicy o wymiarach 8,5 x 11 cali z siatką 1 cala. Ustaw kamerę w odległości 11 cali od szachownicy. Przed zrobieniem zdjęć zablokuj ostrość na szachownicy.

Zrób zdjęcie szachownicy bez okularów do czytania. Następnie, niczego nie ruszając, umieść okulary do czytania przed aparatem i zrób drugie zdjęcie.

Upewnij się, że pozycja aparatu nie zmienia się pomiędzy ujęciami. Jedyne, co powinno się zmienić między dwoma zdjęciami, to obecność obiektywu okularów przed aparatem.

Gdy skończysz ze zdjęciami, prześlij je na swój komputer.

Krok 2: Załaduj obrazy do MATLAB

Otwórz nowy skrypt.

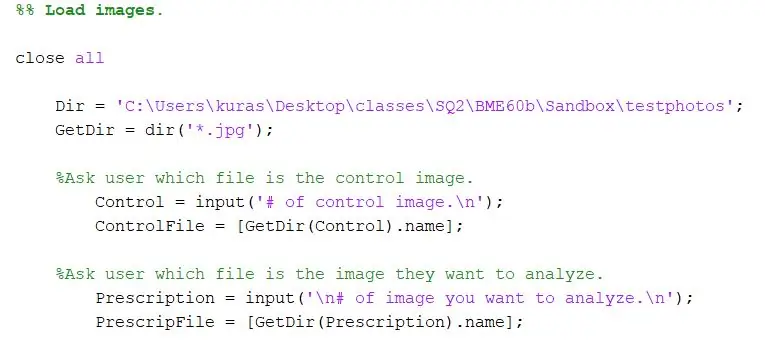
Najpierw określ katalog, w którym przechowywane są zdjęcia. Następnie użyj funkcji dir, aby wyodrębnić obrazy-j.webp

Katalog = 'C:\Użytkownicy\kuras\Desktop\classes\SQ2\BME60b\Sandbox\testphotos'; PobierzKatalog = dir('*.jpg');

W naszym projekcie chcieliśmy podpowiedzieć użytkownikowi programu, z jakimi plikami chce porównać. Pierwsza sekcja prosi użytkownika o określenie obrazu kontrolnego, a druga prosi użytkownika o określenie obrazu testowego.

• % Zapytaj użytkownika, który plik jest obrazem kontrolnym.
• Control = input('# obrazu kontrolnego.\n');
• PlikKontrolny = [PobierzKatalog(Kontrola).nazwa]
• % Zapytaj użytkownika, który plik jest obrazem, który chce analizować.
• ChooseFile = input('\n# obrazu, który chcesz przeanalizować.\n');
• PrescripFile = [GetDir(WybierzPlik).nazwa];

Krok 3: Analiza obrazu

Kolorowy obraz w MATLAB-ie ma rozmiar MxNx3, podczas gdy obraz w skali szarości ma rozmiar MxN. Oznacza to, że ulepszanie/edycja obrazu w skali szarości jest szybsze, ponieważ jest mniej danych do śledzenia. Użyj rgb2gray, aby przekonwertować obraz do skali szarości. (Użyliśmy funkcji imrotate, ponieważ nasze zdjęcia zostały umieszczone poziomo – ta linia kodu może, ale nie musi być potrzebna w Twojej wersji.)

• % przekonwertuj do skali szarości i obróć
• I = imread(PlikKontrolny);
• I = rgb2szary(I);
• I = imrotat(I, 90);

Następnie wyświetl obraz. Funkcja subplot służy do tego, aby obraz testowy mógł znajdować się obok kontrolki w późniejszych krokach.

• %wyświetlacz
• rysunek(1);
• wątek pomocniczy(1, 2, 1)
• imshow(I);
• tytuł(PlikKontrolny);

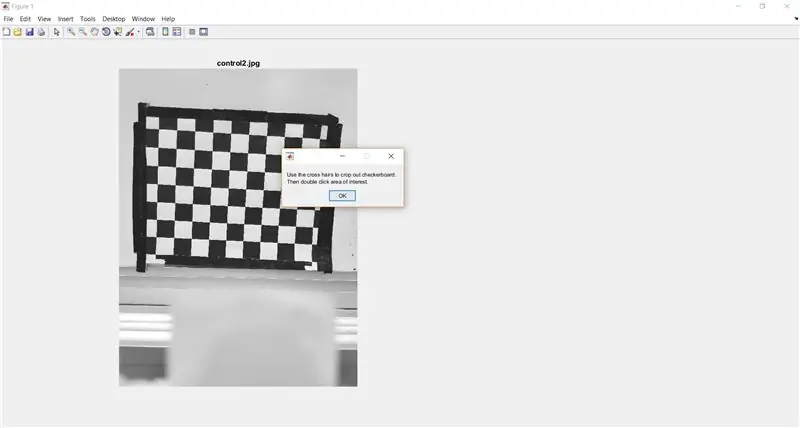
Użyj imcrop, aby poprosić użytkownika o wycięcie szachownicy z pełnego obrazu. Poniższy kod pokazuje również okno komunikatu, aby dostarczyć użytkownikowi instrukcje.

• %wytnij szachownicę do analizy
• waitfor(msgbox({'Użyj krzyżyka, aby wyciąć szachownicę.', 'Następnie kliknij dwukrotnie interesujący obszar.'}));
• I_crop = imcrop(I);

Użyj imbinarize, aby zbinaryzować obraz.

I_binary = imbinaryzacja(I_crop);

Krok 4: Oblicz szerokość białych kwadratów na szachownicy

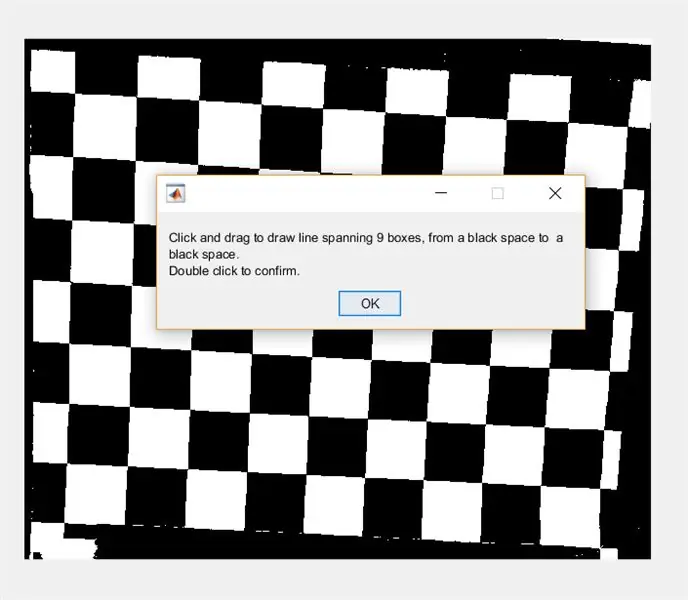
Następnie poproś użytkownika o narysowanie linii w poprzek obrazu za pomocą imline. Linia ta powinna przebiegać poziomo w poprzek szachownicy. Powinien zaczynać się i kończyć na czarnym kwadracie (nie ma znaczenia gdzie) – to dlatego, że będziemy mierzyć szerokość białych kwadratów, a nie czarnych.

• %rysować linię
• figurka(1)
• wątek pomocniczy(1, 2, 1)
• imshow(I_binarny);
• waitfor(msgbox({'Kliknij i przeciągnij, aby narysować linię obejmującą 9 pól, od czarnej przestrzeni do czarnej przestrzeni.', 'Kliknij dwukrotnie, aby potwierdzić.'}));
• linia = imline;
• pozycja = czekaj(linia);
• punkty końcowe = linia.getPosition;

Wyodrębnij współrzędne X i Y dla punktów końcowych narysowanej linii.

• X = punkty końcowe(:, 1)
• Y = punkty końcowe(:, 2);

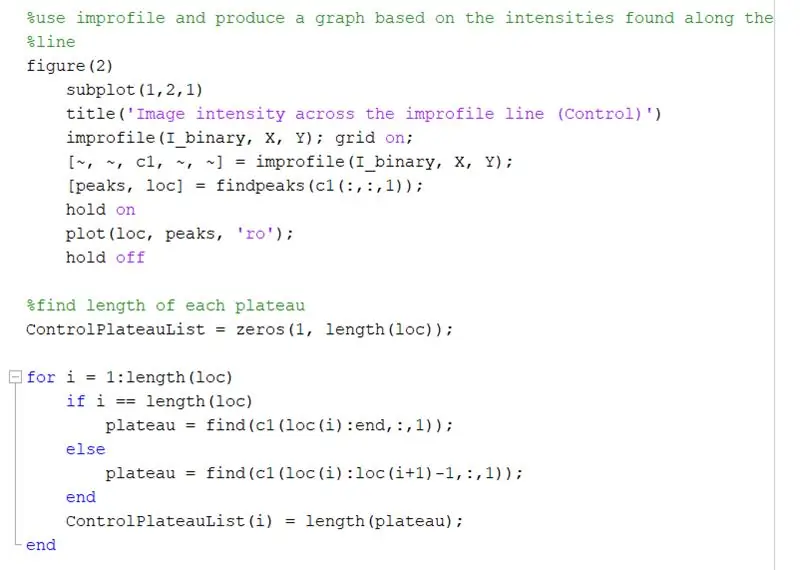
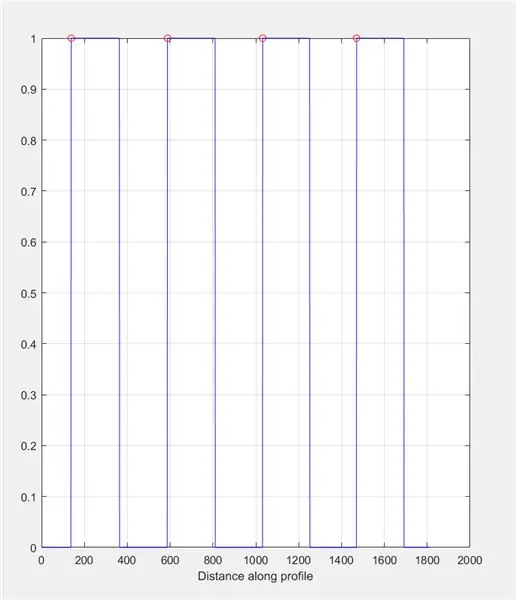
Użyj improfile, aby utworzyć wykres na podstawie intensywności znalezionych wzdłuż narysowanej linii. Powinno to przypominać falę prostokątną o zakresie od 0 (czarny) do 1 (biały). Oblicz szczyty i ich położenie.

• Rysunek 2)
• wątek pomocniczy(1, 2, 1)
• title('Intensywność obrazu w całej linii nieprofilu (kontrola)')
• improfile(I_binarny, X, Y); siatka włączona;
• [~, ~, c1, ~, ~] = improfile(I_binary, X, Y);
• [szczyty, loc] = znajdźszczyty(c1(:,:, 1));
• trzymać się
• działka(loc, szczyty, 'ro');
• wstrzymaj się

Znajdź długość każdego płaskowyżu na wykresie nieprofilu za pomocą pętli for. Uruchom pętlę for dla takiej samej liczby pików, jaka jest na wykresie nieprofilu. Aby obliczyć długość każdego płaskowyżu, użyj funkcji „znajdź”, aby znaleźć wszystkie lokalizacje, w których występuje wartość „1” zamiast „0”. Następnie oblicz długość tej tablicy, aby uzyskać całkowitą długość plateau, która powinna być równa szerokości białego kwadratu w pikselach. ControlPlateauList = zeros(1, length(loc));

dla i = 1:długość(loc)

jeśli i == długość(loc)

plateau = find(c1(loc(i):end,:, 1));

w przeciwnym razie

plateau = znajdź(c1(loc(i):loc(i+1)-1,:, 1));

kończyć się

ControlPlateauList(i) = długość(plateau);

kończyć się

Krok 5: Powtórz kroki 3 i 4 dla obrazu testowego

*Uwaga: rysując nieprofilowaną linię na obrazie testowym, upewnij się, że rysujesz ją w poprzek kwadratów, które odpowiadają linii narysowanej na obrazie kontrolnym.

Krok 6: Oblicz powiększenie soczewki

Powiększone pomiary są obliczane poprzez podzielenie średniej długości plateau, która została obliczona w kroku 5, przez średnią długość plateau kontrolnego, która została obliczona w kroku 4. Jest to obliczane jako 1,0884.

powiększenie = średnia(Lista Plateau)/średnia(Lista Plateau Kontroli);

Krok 7: Znalezienie R-kwadrat i recepty użytkownika za pomocą interpolacji

Za pomocą kodu:

• md1 = fitlm(GivenRescription, MagArray);
• Rkwadrat = md1. Rkwadrat. Zwykły;

Możemy znaleźć wartość R-kwadrat wykresu GivenPresciption (wartości podane przez nasze obiektywy) vs. MagArray (tablica współczynników powiększenia, które obliczyliśmy wcześniej). Mając wystarczająco wysoką wartość R-kwadrat, można wywnioskować, że istnieje wystarczająco silna korelacja, aby uzasadnić zastosowanie tej metody. W tym konkretnym przypadku wartość R-kwadrat wyniosła 0,9912, co sugeruje silną korelację i tym samym uzasadnia stosowanie tej metody w analizie.

Korzystanie z funkcji:

Recepta = interp1(MagArray, GivenPrescription, powiększenie, 'liniowe');

Możemy interpolować odpowiednią wartość recepty (na osi x) naszego współczynnika powiększenia (wartość na osi y) i znaleźć receptę użytkownika.

Interpolacja danych jest ważna, aby ta metoda działała, ponieważ pozwala nam przyjąć założenia dotyczące informacji, których nie posiadamy, na podstawie informacji, które posiadamy. Chociaż linia najlepiej pasująca byłaby technicznie silniejszym kandydatem do tego założenia, tworzenie granic w celu zmniejszenia liczby wyjść służy temu samemu efektowi, ponieważ okulary korekcyjne i tak mają przyrostowe jednolite wartości. Wyjaśniono to w dalszych krokach.

Krok 8: Wyświetlanie recepty użytkownika na wykresie

Używając następującego kodu:

• postać;
• plot(GivenRescription, MagArray, '-g')
• trzymać się
• działka(recepta, powiększenie, 'bp')
• wstrzymaj się
• siatka
• legend('Dane', 'Interpolowane punkty', 'Lokalizacja', 'NW')

Możemy wykreślić wykres, który pokazuje współczynniki powiększenia w porównaniu z daną receptą z zieloną linią i znalezione dane naszego obliczonego powiększenia w porównaniu z naszą interpolowaną receptą z niebieską gwiazdą. Następnie legenda oznacza tytuł, oś x i oś y i umieszcza legendę w lewym górnym rogu.

Krok 9: Zawęź swoją receptę

Poniższy kod służy do zaokrąglenia recepty:

• jeśli Recepta <= 1,125

  Obliczona recepta = '1.0';

• elseif Recepta <= 1,375

  Obliczona recepta = '1,25';

• elseif Recepta <= 1,625

  Obliczona recepta = '1,5';

• elseif Recepta <= 1,875

  Obliczona recepta = '1,75';

• elseif Recepta <= 2,25

  Obliczona recepta = '2.0';

• elseif Recepta <= 2,625

  Obliczona recepta = '2,5';

• elseif Recepta <= 3

  Obliczona recepta = '2,75';

• elseif Recepta <= 3.375

  Obliczona recepta = '3,25';

• w przeciwnym razie

  Obliczona recepta = 'nieznane';

• kończyć się

Recepta znaleziona przez interpolację niekoniecznie odzwierciedla rzeczywistą receptę - dzieje się tak, ponieważ zawsze będą niewielkie różnice w analizie zdjęcia z powodu błędu ludzkiego. Dlatego potrzebujemy tego kroku, aby sklasyfikować rzeczywistą receptę.

Recepty, które są wystawiane zwykle zaczynają się od 1,0 dioptrii i zwiększają się o 0,25 w ich receptach, więc po obliczeniu recepty chcemy określić receptę, która najlepiej odpowiada potrzebom użytkownika. Po wyliczeniu recepty przepuszczamy ją przez podane instrukcje If, aby sprawdzić jej wartość i określić, jaka recepta jest potrzebna. Wszystko mniejsze lub równe 1,125, wtedy recepta wynosi 1,0. Wszystko mniejsze lub równe 1,375, recepta wynosi 1,25. Wszystko mniejsze lub równe 1,625, recepta wynosi 1,5. Wszystko mniejsze lub równe 1,845, recepta wynosi 1,75. I tak dalej.

Mamy wartości rosnące, ponieważ sprawdzamy, czy wartości są mniejsze niż. Jeśli zmniejszymy wartości, to pierwsza instrukcja if będzie czytać pierwszą instrukcję przez cały czas. Jeśli recepta jest najmniejsza, chcemy, aby od razu rozpoznała ją jako najmniejszą, dlatego zaczynaliśmy od najmniejszej wartości. Wszystko, co jest wyższe niż najwyższa wartość, oznacza, że recepta nie mieści się w zakresie naszych danych, więc da odczyt ciągu „Nieznany”.