☠WEEDINATOR☠ Część 4: Kod geometrii różnicowego układu kierowniczego: 3 kroki

2024 Autor: John Day | [email protected]. Ostatnio zmodyfikowany: 2024-01-30 11:32

Jeśli masz czas, aby obejrzeć powyższy film, zauważysz, że pojawiają się dziwne odgłosy powodowane przez silniki na kierownicy, które co jakiś czas gaśnie, gdy WEEDINATOR pokonuje 3-punktowy zakręt. Silniki zasadniczo zacinają się ze sobą, ponieważ promień skrętu jest różny od wewnątrz i na zewnątrz, a odległość, jaką pokonuje koło, jest różna w zależności od stopnia obrotu.

Geometrię skrętu można opracować, naszkicując około 8 permutacji skrętu, podając przykłady skrętu pod różnymi kątami na wewnętrznym kole od 0 (brak skrętu) do 90 (pełna blokada) stopni. Brzmi skomplikowanie?

Większość małych robotów kołowych nie próbuje mieć żadnego wyrafinowanego układu kierowniczego i polega, bardzo skutecznie, po prostu na zmianie względnej prędkości silników po obu stronach pojazdu, co jest prawie takie samo, jak w przypadku gąsienicowej koparki lub czołgu Pracuje. Jest to świetne rozwiązanie, jeśli szarżujesz nad wypełnioną kraterami strefą wojny, strzelając do wszystkiego, co się porusza, ale w spokojnym środowisku rolniczym ważne jest, aby wyrządzić jak najmniej szkód glebie i ziemi, więc ścieranie kół do siebie i do przodu jest nieodpowiednie!

Większość samochodów i traktorów ma bardzo przydatny gadżet zwany „dyferencjałem”, z wyjątkiem samochodów, które można zobaczyć w starych amerykańskich filmach, w których za każdym razem, gdy skręcają za rogiem, słychać jak szalone piszczenie opon. Czy Amerykanie nadal budują takie samochody? Za pomocą WEEDINATORA możemy zaprogramować dyferencjał w silnikach napędowych, wypracowując wzór na względne prędkości i kąty kół przy dowolnym kącie skrętu. Nadal brzmi skomplikowanie?

Oto krótki przykład:

Jeśli WEEDINATOR porusza się po zakręcie i ma wewnętrzne koło pod kątem 45 stopni, zewnętrzne koło NIE ma 45 stopni, to bardziej jak 30 stopni. Również koło wewnętrzne może obracać się z prędkością 1 km/h, ale koło zewnętrzne będzie znacznie szybsze, bardziej jak 1,35 km/h.

Krok 1: Konfiguracja geometrii

Na początek przyjmuje się kilka podstawowych założeń:

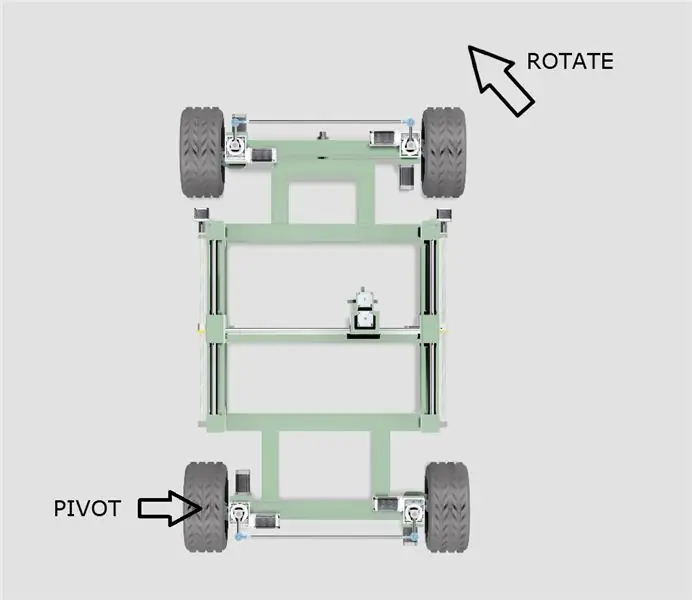
• Podwozie obróci się wokół jednego z tylnych kół, jak pokazano na powyższym schemacie.
• Efektywny środek okręgu obrotowego będzie przesuwał się wzdłuż linii rozciągającej się od środków dwóch tylnych kół, w zależności od kąta skrętu.
• Geometria przyjmie formę krzywej sinusoidalnej.

Krok 2: Skalowane rysunki kątów i promieni kół

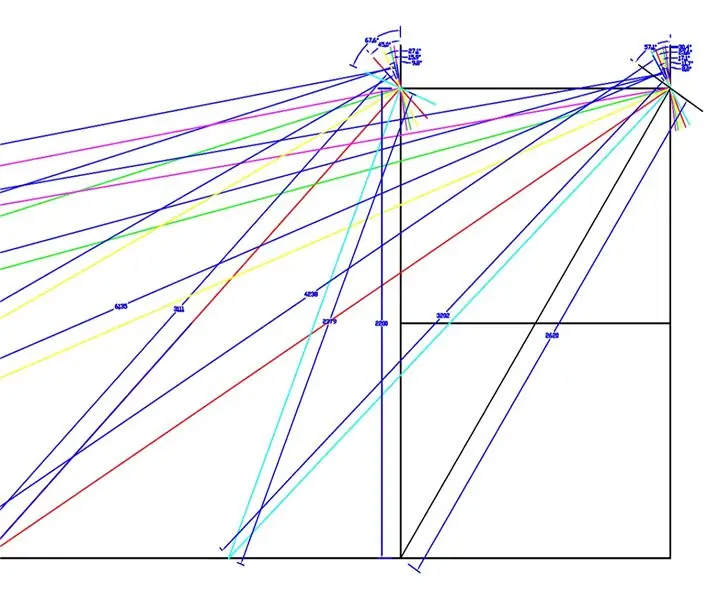
Wykonano rysunek w pełnej skali przednich kół i podwozia WEEDINATOR z 8 różnymi permutacjami kąta wewnętrznego kół od 0 do 90 stopni, a odpowiednie środki skrętu zostały odwzorowane, jak pokazano na powyższych rysunkach.

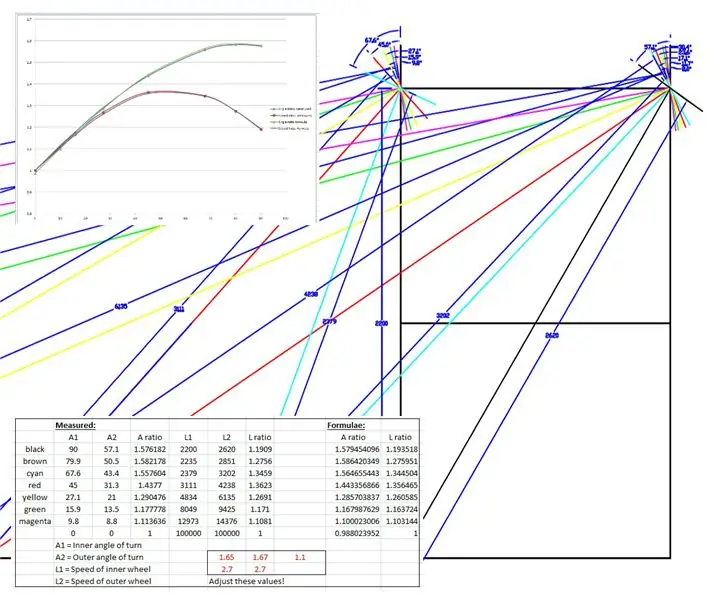
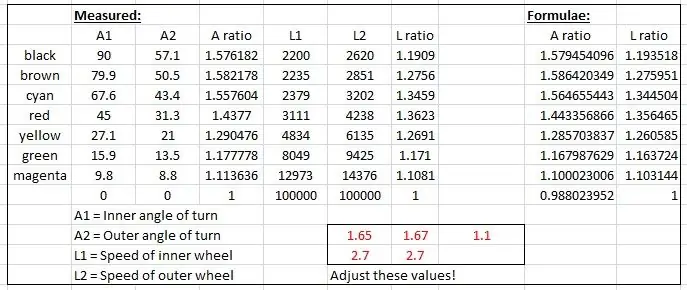
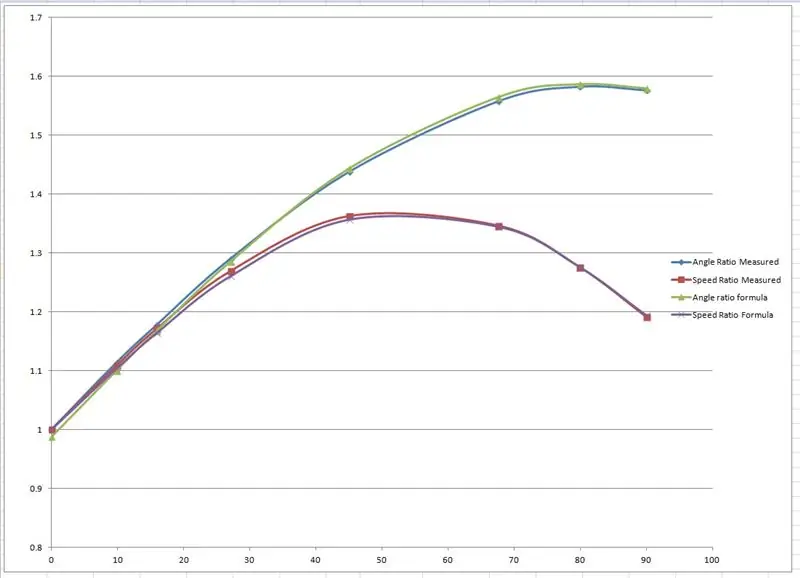
Efektywne promienie zmierzono z rysunku i wykreślono na wykresie w programie Microsoft Excel.

Utworzono dwa wykresy, jeden przedstawiający stosunek lewego i prawego przedniego koła, a drugi stosunek dwóch promieni dla każdego konkretnego kąta skrętu.

Następnie "sfałszowałem" kilka wzorów, aby naśladować wyniki empiryczne oparte na krzywej sinusoidalnej. Jedna z krówek wygląda tak:

współczynnik prędkości= (sin(wewnętrzny*1,65*pi/180)+2,7)/2,7; // wewnętrzny to wewnętrzny kąt skrętu.

Krzywe zostały uformowane przez zmianę wartości pokazanych na czerwono w pliku Excel, aż krzywe do siebie pasują.

Krok 3: Kodowanie formuł

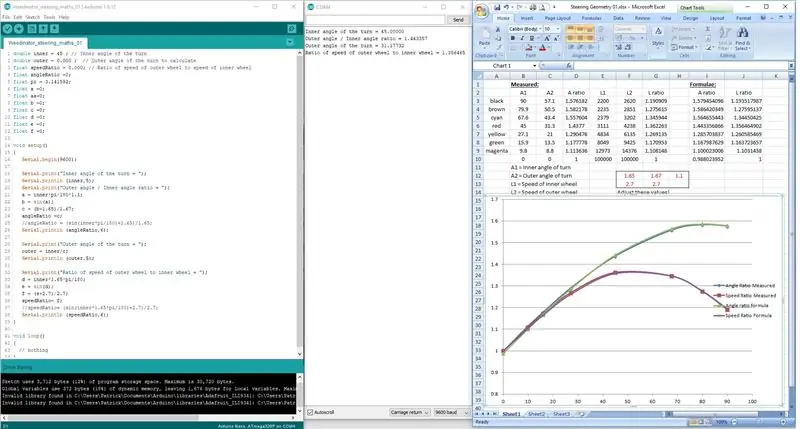
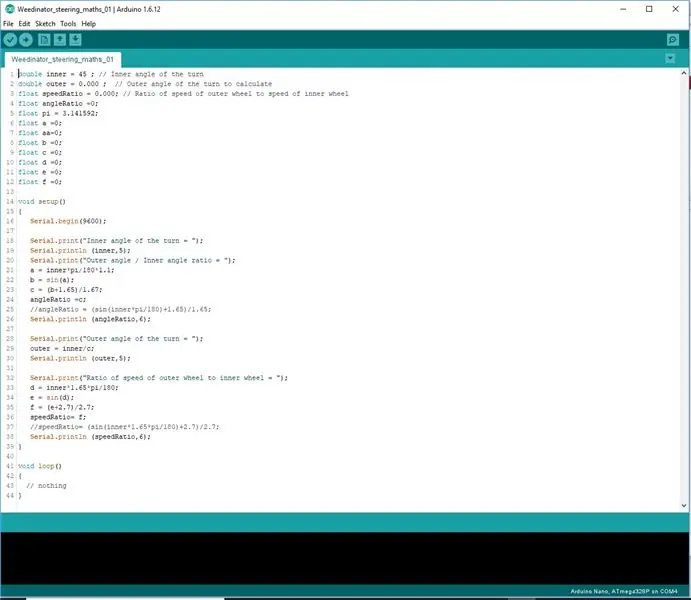
Zamiast próbować kodować formuły w jednym wierszu, zostały one podzielone na 3 etapy, aby umożliwić Arduino prawidłowe przetwarzanie danych matematycznych.

Wyniki są wyświetlane na wyświetlaczu portu szeregowego i sprawdzane z wynikami pomiarów na rysunku w skali.