Eksperymenty z zaawansowanym rejestrowaniem danych (przy użyciu Pythona): 11 kroków

2024 Autor: John Day | [email protected]. Ostatnio zmodyfikowany: 2024-01-30 11:27

Istnieje wiele instrukcji dotyczących rejestrowania danych, więc kiedy chciałem zbudować własny projekt rejestrowania, rozejrzałem się po kilku. Niektóre były dobre, inne nie, więc postanowiłem wziąć kilka lepszych pomysłów i stworzyć własną aplikację. Zaowocowało to projektem zarówno bardziej zaawansowanym, jak i bardziej skomplikowanym, niż się początkowo spodziewałem. Jedną z jego części stała się seria eksperymentów w przetwarzaniu danych z czujników. Ta instrukcja pozwala wypróbować te same lub podobne eksperymenty.

(Możesz zobaczyć cały kod i pobrać go pod adresem: Kod na GitHub Możesz przejść do przeglądania, być może w innym oknie, za pomocą zaledwie 2 kliknięć)

Zazwyczaj rejestrowanie danych obejmuje:

• Akwizycja danych: Odczytaj dane z czujnika. Często jest to po prostu odczyt przetwornika analogowo-cyfrowego (ADC) na urządzeniu takim jak Arduino.
• Przetwarzanie danych: Podczas odczytu wartości ADC, wyjście przetwornika musi być przeskalowane do właściwych jednostek. Może zaistnieć również potrzeba wykonania pewnej regulacji w celu skalibrowania wartości w celu skorygowania błędów czujnika.
• Filtrowanie: Dane zwykle zawierają trochę szumu, który można filtrować, aby szukać sygnału w danych, a nie szumu.
• Przechowywanie danych: dane są zapisywane, być może w pliku tekstowym, może w chmurze. Dane powinny przetrwać nawet po wyłączeniu zasilania. Łatwo jest zapisać zbyt dużo danych, mamy małą sztuczkę, aby zmniejszyć przestrzeń do przechowywania danych.
• Wyświetlanie danych: Metody przeglądania danych, a nie rejestrowanie danych, ale jeśli nie wyświetlasz danych, po co je zbierać?
• Zdalny dostęp: nie jest konieczny, ale fajnie go mieć.

Większość instrukcji zawiera niektóre, ale nie wszystkie z powyższych, lub wykonuje je w bardzo prosty sposób. Ta instrukcja rozwiąże 2 z często pomijanych problemów z logowaniem, a jako bonus da ci możliwość tworzenia wykresów danych bez korzystania z usługi w chmurze. Możesz użyć całości lub wyciągnąć fragmenty i zmiksować je w swój własny projekt.

Krok 1: Narzędzia i materiały

Ten przykład jest w całości w Pythonie, więc będzie działał, a komponenty mogą być używane na prawie każdym systemie operacyjnym, w tym Mac, PC, Linux i Raspberry Pi.

Aby skorzystać z tej instrukcji, potrzebujesz tylko działającego środowiska Python 3.6 i pobierz załączony kod. Po uruchomieniu utworzonego przeze mnie kodu możesz go modyfikować do własnych eksperymentów. Jak zwykle w Pythonie, może być konieczne dodanie kilku pakietów/modułów, aby wszystko działało. Moje środowisko Spyder zawiera prawie wszystkie wymagane części (patrz: Graficzne widoki instruktażowe z Python Screen Scraping). Kiedy po raz pierwszy uruchomisz obserwację wszelkich komunikatów o błędach, poinformują Cię o brakujących częściach w Twoim środowisku.

W kolejnych dwóch krokach dowiesz się, jak utworzyć i przeprowadzić własny eksperyment, ale prawdopodobnie lepiej poczekać, aż uruchomisz dołączone eksperymenty, zanim spróbujesz własnego.

Aby zrozumieć kod, musisz mieć trochę doświadczenia z Pythonem zorientowanym obiektowo, wyjaśniając, że wykracza to poza zakres tej instrukcji, ale Google powinien udzielić ci wszelkiej pomocy, której możesz potrzebować.

Zwróć uwagę na kod: (Kod na GitHub Możesz przejść do przeglądania, być może w innym oknie, za pomocą zaledwie 2 kliknięć) jest teraz w Pythonie 3.6, więc posiadanie 3.6 byłoby najlepsze. Starsza wersja kodu znajduje się tutaj w linkach poniżej.

Krok 2: Budowanie eksperymentu

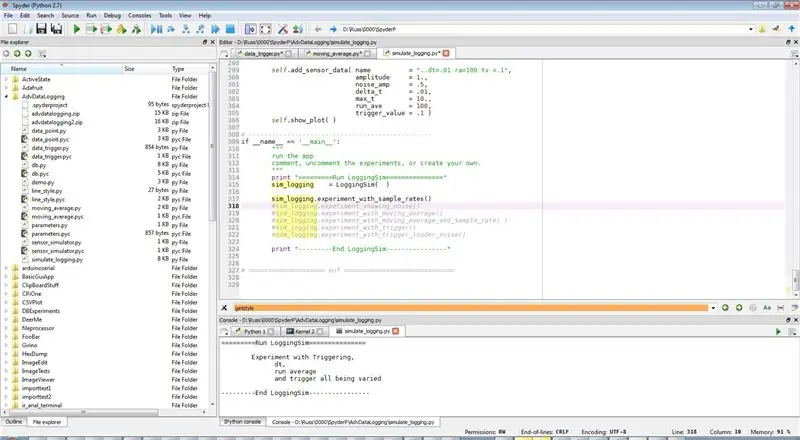
Istnieją trzy kroki programowania (i linie) w tworzeniu eksperymentu. Każdy eksperyment jest funkcją w obiekcie LoggingSim w pliku symulacja_logowania.py. Spójrzmy na eksperyment 1 (tylko pierwszy wykres), który przeprowadzimy w następnym kroku:

def eksperyment_z_przykładowymi_stawkami(samo):

print """ Eksperyment z częstotliwościami próbkowania Patrzenie na różne częstotliwości próbkowania poprzez zmianę delta T """ self.start_plot(plot_title = "Częstotliwości próbkowania - Część 1/3: Delta T = 1.0") self.add_sensor_data(name = "dt = 1.", amplituda = 1., noise_amp =.0, delta_t = 1., max_t = 10., run_ave = 0, trigger_value = 0) self.show_plot()

Każdy eksperyment jest napisany jako osobna funkcja, więc mamy linię definiującą funkcję (def eksperyment…..)

Następna linia bez komentarza (start_plot(….) tworzy obiekt dla eksperymentu i nadaje mu nazwę.

Następna linia bez komentarza (add_sensor_data(…) jest podzielona na kilka linii. Symuluje czujnik mierzący sygnał z potencjalnym szumem i pewnym przetwarzaniem. Argumenty funkcji są następujące:

• nazwa: nazwa umieszczana na ostatnim wykresie w celu identyfikacji danych
• amplituda: jak duży jest sygnał, zawsze będziemy używać amplitudy 1. w tej instrukcji.
• noise_amp: jak duży jest hałas, 0. nie ma hałasu, zaczniemy tutaj.
• delta_t: czas między pomiarami, kontroluje częstotliwość próbkowania.
• max_t: maksymalny czas zbierania danych, zawsze użyjemy 10 w tej instrukcji.
• run_ave: przetwarzanie przy użyciu średniej kroczącej, 0 oznacza brak przetwarzania.
• trigger_value: przetwarzanie za pomocą wyzwalania, 0 oznacza brak przetwarzania

ostatnia linia bez komentarza (self.show_plot……) wyświetla wykres.

Aby nieco skomplikować sprawę, możesz mieć wiele linii na wykresie lub wiele wykresów w eksperymencie, co powinno jasno wynikać z poniższych eksperymentów.

Krok 3: Przeprowadzanie eksperymentu

To jest kod do przeprowadzenia eksperymentu. Jak zwykle w Pythonie, jest on umieszczany na końcu pliku.

sim_logging = RejestrowanieSim()

sim_logging.experiment_with_sample_rates()

To tylko 2 linie:

• Utwórz symulator rejestrowania (LoggingSim())
• Uruchom go (sim_logging.experiment_with_sample_rates())

W pobranym kodzie mam jeszcze kilka linijek i komentarzy, powinno to być łatwe do rozgryzienia.

Krok 4: Eksperyment: Częstotliwość próbkowania

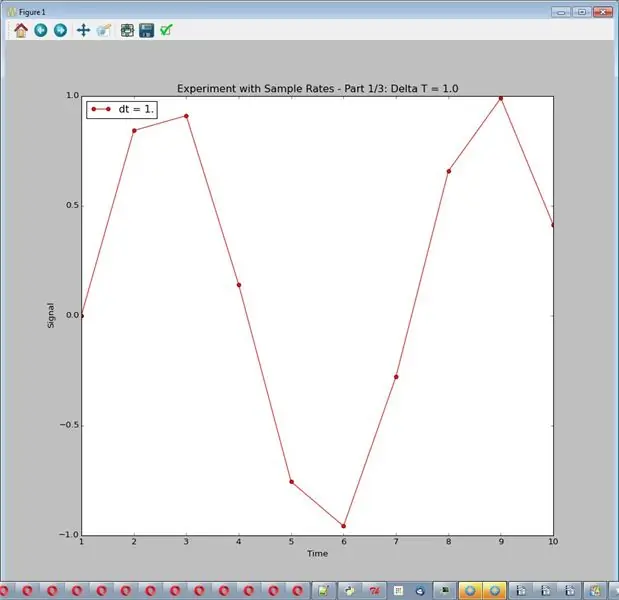
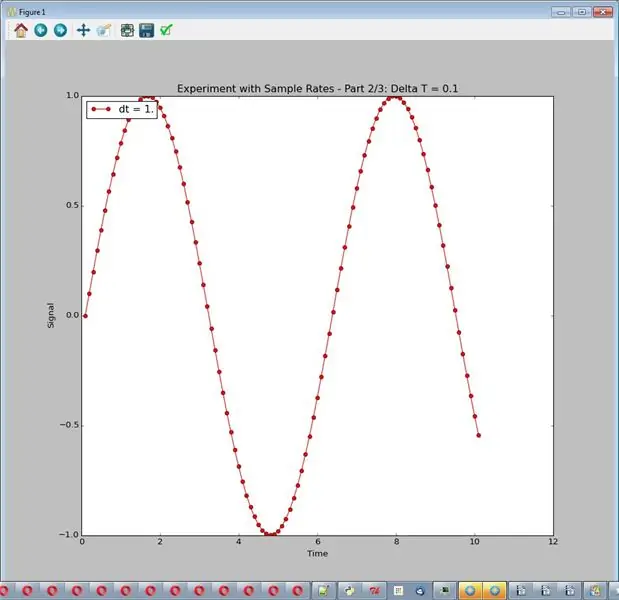
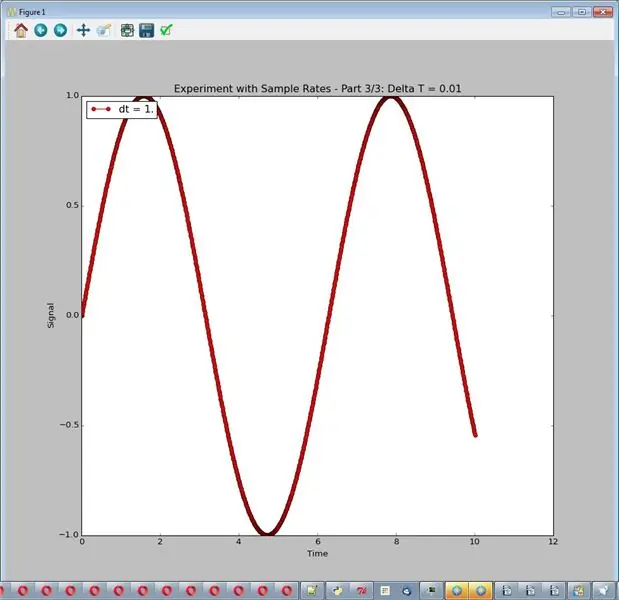
Symulator, jak tutaj skonfigurowano, zawsze generuje ładną, gładką sinusoidę o amplitudzie 1. W tym eksperymencie będziemy mieszać z częstotliwością próbkowania, dostosowaną przez delta_t, różnicę czasu między próbkami. Nie będziemy mieć żadnego hałasu ani innego przetwarzania. Kod wykorzystuje 3 częstotliwości próbkowania (delta_t = 1,0, 0,1 i 0,01). Ponieważ wykresy leżą jeden na drugim, eksperyment jest skonfigurowany tak, aby wygenerować 3 różne wykresy. Otrzymane wykresy są obrazami dla tego kroku.

def eksperyment_z_przykładowymi_stawkami(samo):

print """ Eksperyment z częstotliwościami próbkowania Patrzenie na różne częstotliwości próbkowania poprzez zmianę delta T """ self.start_plot(plot_title = "Eksperyment z częstotliwościami próbkowania 1/3: Delta T = 1.0") self.add_sensor_data(name = "dt = 1.", amplituda = 1., wzmacniacz_szumu =.0, delta_t = 1., max_t = 10., run_ave = 0, wartość_wyzwalacza = 0) self.show_plot() # ----------------- ----------------------------------- self.start_plot(plot_title = "Częstotliwość próbkowania eksperymentu 2/3: Delta T = 0.1") self.add_sensor_data(name = "dt = 1.", amplituda = 1., noise_amp =.0, delta_t = 0.1, max_t = 10., run_ave = 0, trigger_value = 0) self.show_plot() # ------------------------------------------------ samego siebie.start_plot(plot_title = "Częstotliwości próbkowania eksperymentu 3/3: Delta T = 0.01") self.add_sensor_data(name = "dt = 1.", amplituda = 1., noise_amp =.0, delta_t = 0.01, max_t = 10., run_ave = 0, trigger_value = 0) self.show_plot()

Aby go uruchomić użyj linii: sim_logging.experiment_with_sample_rates()

Możliwe wnioski:

• Zbyt niska częstotliwość próbkowania jest naprawdę zła.
• Wysokie stawki są często lepsze.

(Kod Pythona 3.6 w linku GitHub poniżej w instrukcjach, 2.7)

Krok 5: Eksperyment: pokazywanie hałasu

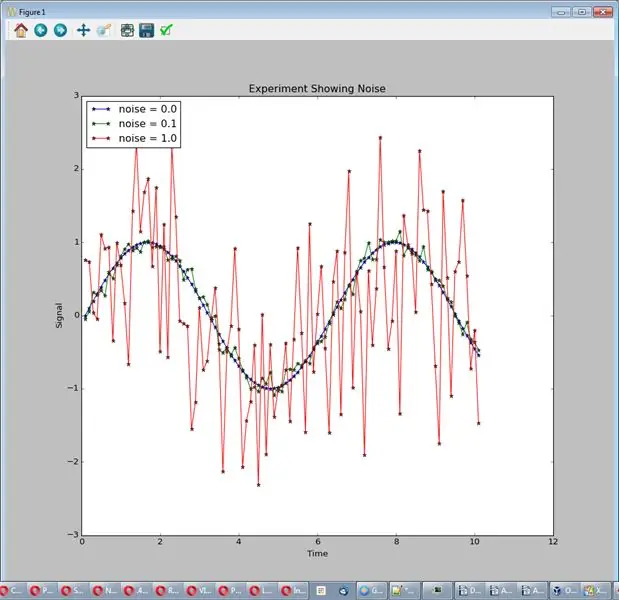
W tym eksperymencie utrzymujemy ten sam sygnał, używamy średniej częstotliwości próbkowania i mamy różne ilości szumu (noise_amp =.0,.1, 1.0.) Uruchom to za pomocą: sim_logging.experiment_showing_noise(). Wynikiem jest jeden wykres z 3 liniami.

Możliwy wniosek:

Hałas utrudnia dostrzeżenie sygnału, zmniejsz go, jeśli możesz

Kod:

# ------------------------------------------------

def eksperyment_showing_noise(self): print """ Eksperyment pokazujący szum Patrzenie na różne ilości szumu poprzez zmianę amplitudy szumu. """ self.start_plot(plot_title = "Eksperyment pokazujący szum") self.add_sensor_data(name = "noise = 0.0 ", amplituda = 1., wzmacniacz_szumu =.0, delta_t =.1, max_t = 10., run_ave = 0, wartość_wyzwalacza = 0) self.add_sensor_data(name = "noise = 0.1", amplituda = 1., wzmacniacz_szumu =. 1, delta_t =.1, max_t = 10., run_ave = 0, trigger_value = 0) self.add_sensor_data(name = "noise = 1.0", amplituda = 1., noise_amp = 1., delta_t =.1, max_t = 10., run_ave = 0, trigger_value = 0) self.show_plot()

Krok 6: Eksperyment: zmniejsz hałas za pomocą średniej ruchomej

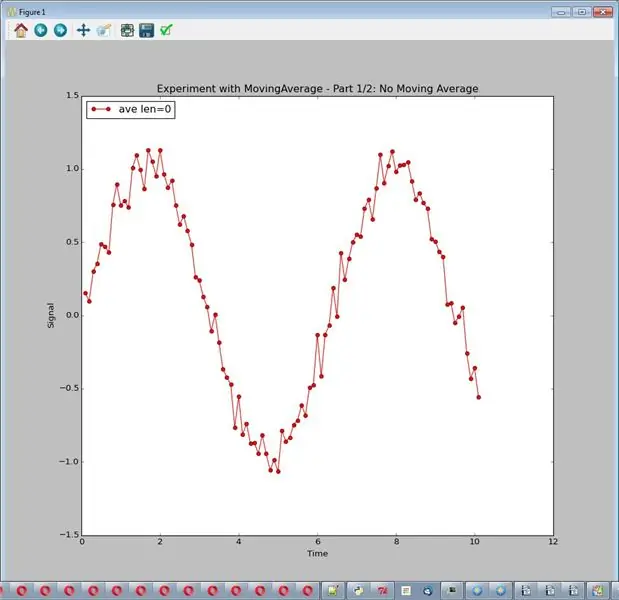
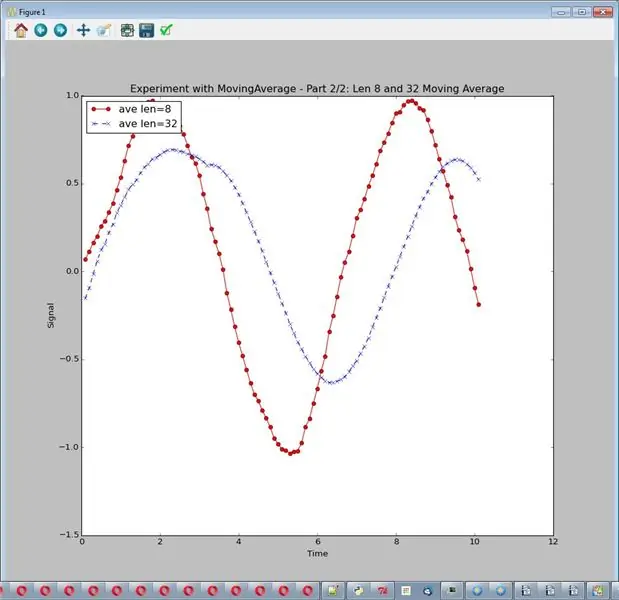
Średnia ruchoma (na przykład o długości 8) wykonuje ostatnie 8 pomiarów i uśrednia je. Jeśli szum jest losowy, mamy nadzieję, że wyniesie około 0. Przeprowadź eksperyment za pomocą: sim_logging.experiment_showing_noise(). Wydrukuj jeden wykres.

Możliwe wnioski:

• Średnia ruchoma eliminuje większość hałasu
• Im dłuższa średnia ruchoma, tym większa redukcja szumów
• Dłuższa średnia ruchoma może zmniejszyć i zniekształcić sygnał

Kod:

# ------------------------------------------------

def eksperyment_with_moving_average(self): print """ Eksperymentuj z MovingAverage Patrząc na różne MovingAverage zmieniając długość. Wszystkie mają ten sam szum. """ # ------------------ ------------------------------ self.start_plot(plot_title = "Średnia ruchoma-część 1/2: brak średniej ruchomej").add_sensor_data(name = "ave len=0", amplituda = 1., noise_amp =.1, delta_t =.1, max_t = 10., run_ave = 0, trigger_value = 0) self.show_plot() self.start_plot(plot_title = "MovingAverage-Part 2/2: Len 8 and 32") self.add_sensor_data(name = "ave len=8", amplituda = 1., noise_amp =.1, delta_t =.1, max_t = 10., run_ave = 8, trigger_value = 0) self.add_sensor_data(name = "ave len=32", amplituda = 1., noise_amp =.1, delta_t =.1, max_t = 10., run_ave = 32, trigger_value = 0) self.show_plot ()

Krok 7: Eksperyment: średnia ruchoma i częstotliwość próbkowania

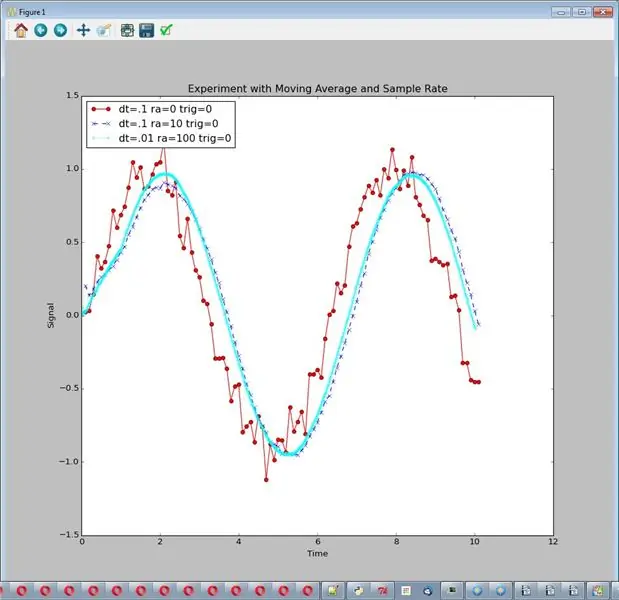
W tym eksperymencie porównujemy surowy sygnał z szumem i 2 różnymi wariacjami dotyczącymi redukcji szumu.

1. Średnia częstotliwość próbkowania i średnia ruchoma
2. Wysoka częstotliwość próbkowania i średnia ruchoma o dużej długości

Uruchom to za pomocą: sim_logging…… Wynikiem jest jeden wykres. Myślę, że jasne jest, że #2 lepiej radzi sobie z redukcją hałasu, więc możemy dojść do wniosku, że:

Wysoka częstotliwość próbkowania i średnia ruchoma o dużej długości są dobre

Ale musisz pamiętać, że jest koszt. #2 zajmuje dużo więcej przetwarzania i skutkuje znacznie większą ilością danych do zapisania. Koszt może, ale nie musi być tego wart. W następnym eksperymencie dodamy wyzwalacz, czyli urządzenie zmniejszające ilość przechowywanych danych.

Kod:

def eksperyment_z_ruchami_średnią_i_przykładową_współczynnik(self):

print """ Eksperyment ze średnią ruchomą i częstotliwością próbkowania, dt, zróżnicowana średnia przebiegu """ # ---------------------------- -------------------- self.start_plot(plot_title = "Średnia ruchoma i częstotliwość próbkowania") self.add_sensor_data(name = "dt=.1 ra=0 trig= 0", amplituda = 1., noise_amp =.1, delta_t =.1, max_t = 10., run_ave = 0, trigger_value = 0) self.add_sensor_data(name = "dt=.1 ra=10 trig=0", amplituda = 1., noise_amp =.1, delta_t =.1, max_t = 10., run_ave = 10, trigger_value = 0) self.add_sensor_data(name = "dt=.01 ra=100 trig=0", amplituda = 1., noise_amp =.1, delta_t =.01, max_t = 10., run_ave = 100, trigger_value = 0) self.show_plot()

Krok 8: Eksperyment: rejestrowanie za pomocą wyzwalacza

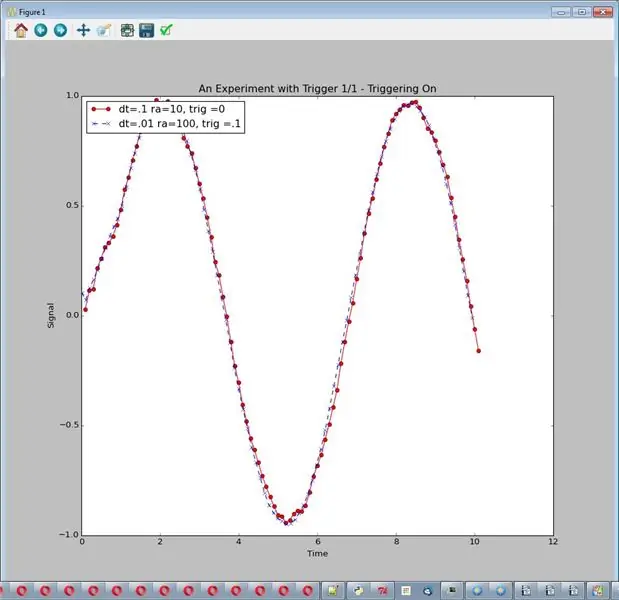
W tym eksperymencie dodajemy wyzwalacz. Po pierwsze, co rozumiem przez wyzwalacz? Wyzwalacz to technika, w której zbieramy dane, ale zapisujemy je dopiero po znaczącej zmianie pewnej zmiennej. W tych eksperymentach ustawiłem wyzwalacz na zmienną czasu (oś x). Używając wyzwalacza, mogę pobrać dużą ilość danych z szybkiego próbkowania i zredukować je do bardziej rozsądnej ilości danych. Jest to szczególnie przydatne przy wysokich częstotliwościach próbkowania i długiej średniej.

Wziąłem wiersz nr 2 z ostatniego eksperymentu, który był „dobry” i dodałem wyzwalacz. Uruchom to za pomocą: sim_logging…… Wyjście to jeden wykres, x linii.

Co się dzieje? Otrzymujemy „dobry” wykres z rozsądną ilością danych (tak samo jak #1). Wyższe przetwarzanie wiązało się z pewnymi kosztami. Ogólnie jednak wyniki są mniej więcej takie same jak nr 1 przy niższej częstotliwości próbkowania przy mniejszym filtrowaniu. Możesz wywnioskować:

• Długotrwała średnia z wyzwalaniem może zapewnić dobrą redukcję szumów przy rozsądnych ilościach danych.
• Dodatkowe przetwarzanie może nie dać o wiele lepszych wyników i wiąże się z kosztami.

Kod:

# ------------------------------------------------

def eksperyment_with_trigger(self): print """ Eksperymentuj z wyzwalaniem, dt, średnią przebiegu i wyzwalaniem wszystkich zmiennych """ # ----------------------- ------------------------- self.start_plot(plot_title = "Wyzwalanie 1/1 - Wyzwalanie włączone") self.add_sensor_data(name = "dt=.1 ra=10, trig =0", amplituda = 1., noise_amp =.1, delta_t =.1, max_t = 10., run_ave = 10, trigger_value = 0) self.add_sensor_data(name = "dt=.01 ra=100, trig =.1", amplituda = 1., noise_amp =.1, delta_t =.01, max_t = 10., run_ave = 100, trigger_value =.1) self.show_plot()

=

Krok 9: Eksperyment: rejestrowanie za pomocą wyzwalacza - głośniejszy hałas

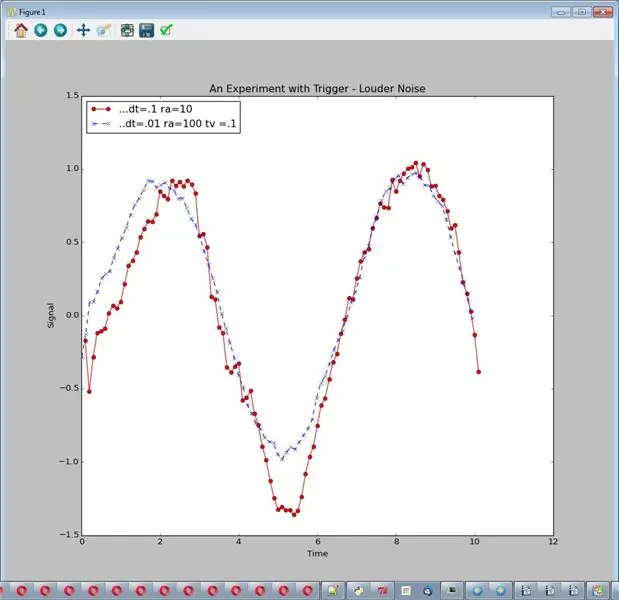
Zróbmy ten sam eksperyment, co w ostatnim kroku i wzmocnijmy hałas. Uruchom to za pomocą: sim_logging…… Wyjście to jeden wykres, 2 linie.

Teraz dodatkowe przetwarzanie wydaje się bardziej opłacalne. Rozsądnym wnioskiem może być tutaj:

Wybór ilości i rodzaju przetwarzania w celu redukcji szumów zależy od sygnału i szumu

Kod:

def expert_with_trigger_louder_noise(self):

print """ Głośniejszy hałas niż w poprzednim eksperymencie """ self.start_plot(plot_title = "Eksperyment z wyzwalaniem - głośniejszy hałas") self.add_sensor_data(name = "…dt=.1 ra=10", amplituda = 1., noise_amp =.5, delta_t =.1, max_t = 10., run_ave = 10, trigger_value = 0) self.add_sensor_data(name = "..dt=.01 ra=100 tv =.1", amplituda = 1., noise_amp =.5, delta_t =.01, max_t = 10., run_ave = 100, trigger_value =.1) self.show_plot()

Krok 10: Wykonaj własne eksperymenty

W tym momencie mam nadzieję, że widzisz, że techniki opisane w tej instrukcji mogą być przydatne w rejestrowaniu danych, ale muszą być również używane z pewną myślą. Eksperymentowanie z nimi może pomóc w tym procesie.

Kilka uwag na temat eksperymentów i rzeczy, którym możesz się przyjrzeć:

• Fale sinusoidalne nie są jedynym interesującym typem sygnału, wypróbuj inne, inne fale lub rampy lub…..
• Użyłem rozkładu normalnego dla hałasu, jest tak wiele rodzajów hałasu; powinieneś rozważyć innych
• Średnie biegowe to prosta, ale nie jedyna metoda patrzenia na hałas

Uwaga: logowanie zdjęć z Wikipedii.

Krok 11: Korzystanie z technik w oprogramowaniu do rejestrowania

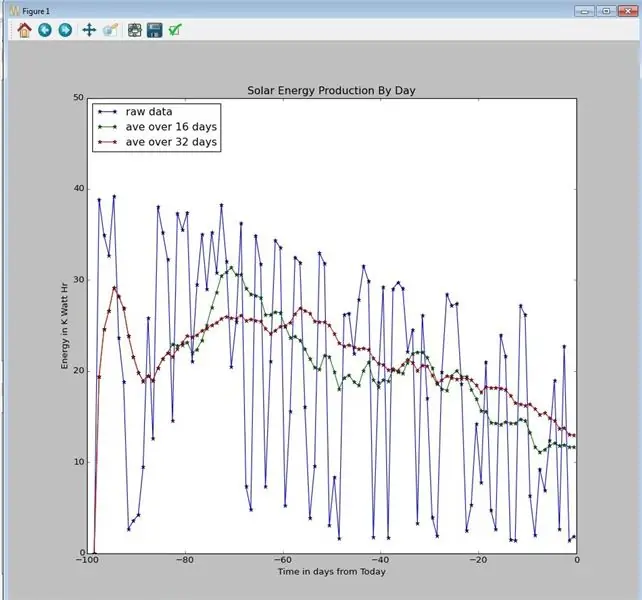
Mój kod jest zorientowany obiektowo, a przetwarzanie dla średniej bieżącej i wyzwalacza można po prostu skopiować do środowiska Pythona, a następnie użyć. Obiektami są:

• DataTrigger w data_trigger.py
• Średnia ruchoma w ruchoma_średnia.py

Mój główny obiekt LoggingSim w symulacji_logging.py powinien dać dobry przykład, jak go używać. Jeśli używasz innego języka, możesz przeczytać mój kod i zaimplementować go w swoim języku.

Ten kod może zapewnić Twojemu projektowi lepsze rejestrowanie danych, wypróbuj go.

Powyższy wykres pochodzi z Graph Your Solar Power autorstwa russ_hensel, który używa tego samego obiektu średniej kroczącej.