
Spisu treści:
- Krok 1: Obwód
- Krok 2: Napęd liniowy
- Krok 3: Bęben
- Krok 4: Wskazówki konstrukcyjne
- Krok 5: Algorytm rysowania linii Bresenhama
- Krok 6: Kodeks
- Krok 7: Menu
- Krok 8: Kalibracja
- Krok 9: Wstępne przetwarzanie Gcode
- Krok 10: Wyniki
- Krok 11: Aktualizacja kodu
- Krok 12: Drum_plotter_v3.ino
- Krok 13: Drum_plotter_plotter_v4.ino
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 11:30.
- Ostatnio zmodyfikowany 2025-01-23 15:03.



Ta instrukcja opisuje ploter A4/A3 wykonany z odcinka plastikowej rury, dwóch silników krokowych BYJ-48 i serwa SG-90. Zasadniczo jest to ploter płaski zwinięty w bęben.
Jeden silnik obraca bęben, podczas gdy drugi porusza głowicą drukującą. Serwo służy do podnoszenia i opuszczania pióra.
Ploter ten ma szereg zalet w stosunku do tradycyjnego plotera płaskiego:
- znacznie mniejszy ślad
- wymaga tylko jednej prowadnicy liniowej
- prosty w budowie
- tani
Wbudowany interpreter akceptuje dane wyjściowe gcode z Inkscape.
Komunikacja z ploterem odbywa się poprzez łącze bluetooth.
Ploter jest kompatybilny z tabletem graficznym CNC opisanym w mojej instrukcji
Chociaż nie jest to precyzyjny instrument, dokładność tego plotera jest zadowalająca dla jego zamierzonego celu przenoszenia konturów akwareli na papier.
Krok 1: Obwód
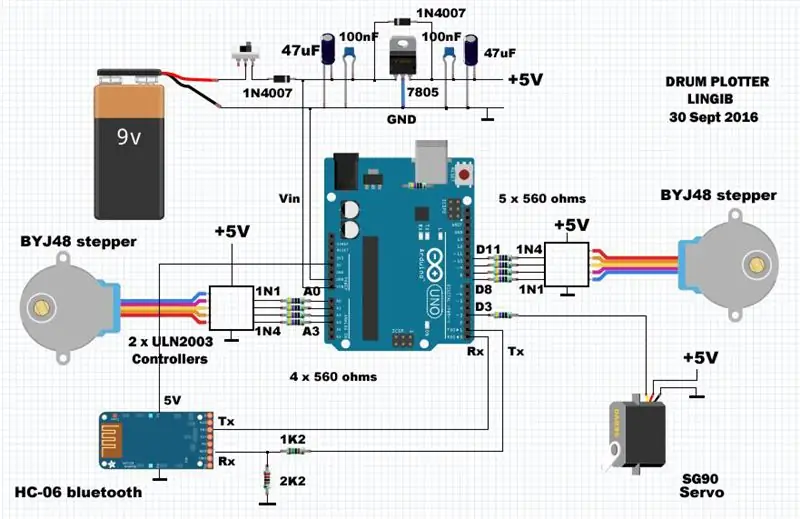
Układ składa się z mikrokontrolera Arduino UNO R3 oraz niestandardowego nakładki, na której montowane są dyskretne elementy. Zasilanie jest dostarczane przez zewnętrzny regulator 5 V 1 A. Średni prąd wynosi około 500mA.
Silniki krokowe BYJ-48 są podłączone do PORTB (piny D8, D9, D10, D11) i PORTC (piny A0, A1, A2, A3). Serwo podnoszące pióro SG-90 jest przymocowane do pinu D3.
Rezystory 560 omów, które można pominąć, zapewniają ochronę arduino przed zwarciem, gdyby coś poszło nie tak. Ułatwiają również okablowanie ekranu, ponieważ działają jak „zworki” na szynach zasilających.
Rezystory 1k2 i 2K2 zapobiegają uszkodzeniu modułu bluetooth HC-06 [1], obniżając napięcie wyjściowe 5 V z arduino do 3,3 V.
[1] Odłącz moduł bluetooth HC-06 podczas wgrywania kodu do arduino przez port USB. Pozwoli to uniknąć konfliktów portów szeregowych.
Krok 2: Napęd liniowy



Napęd liniowy składa się z pręta aluminiowego o długości 3mm x 32mm, paska blachy aluminiowej oraz czterech małych kół pasowych z łożyskami kulkowymi.
Aluminium jest dostępne w większości sklepów z narzędziami. Koła pasowe U624ZZ 4x13x7mm z rowkiem w kształcie litery U są dostępne na stronie
Proste narzędzia ręczne to wszystko, czego potrzebujesz. Przytnij listwę aluminiową, aby dopasować ją do wymiarów plotera.
Zespół silnika
Zamontuj silnik krokowy BJY-48 przez pręt na jednym końcu i przymocuj koło pasowe GT2 20 z otworem 5 mm do wału silnika. Teraz zamontuj kolejne koło pasowe GT2 na drugim końcu pręta tak, aby koło pasowe mogło się swobodnie obracać. Aby to osiągnąć, użyłem rurki (radiowej) o średnicy 5 mm i śruby 3 mm.
Teraz owiń pasek rozrządu GT2 wokół kół pasowych. Połącz końce paska rozrządu za pomocą półskrętu tak, aby zęby przełożyły się na siebie i przymocuj opaską kablową.
Na koniec przymocuj zespół wózka do paska rozrządu za pomocą opaski kablowej.
Zespół karetki
Zespół wózka wykonany jest z paska blachy aluminiowej [1], do którego przykręcone są koła pasowe U624ZZ. W razie potrzeby użyj podkładki 4 mm, aby oddzielić koła pasowe od blachy aluminiowej.
Kółka, które mają rowek 4 mm, obejmują górną i dolną część aluminiowej belki tak, że nie ma pionowego ruchu, a aluminiowa listwa porusza się swobodnie w lewo i prawo.
Aby zapewnić swobodne poruszanie się karetki, najpierw zamontuj dwa górne bloczki, a następnie, trzymając bloczki na pręcie, zaznacz pozycje dwóch dolnych bloczków. Teraz można wywiercić otwory na te dwa koła pasowe. Najpierw użyj małego wiertła „pilotażowego”, aby zapobiec dryfowaniu większego wiertła 4 mm.
Przed zgięciem paska aluminiowego w „U” wywierć otwór na górze i na dole, aby dopasować go do średnicy długopisu. Teraz dokończ zakręty.
Przymocuj pasek rozrządu do zespołu wózka za pomocą opaski zaciskowej i śruby 3 mm między dwoma górnymi kołami pasowymi.
Zespół podnośnika pióra
Przymocuj serwo SG-90 do górnej części zespołu wózka za pomocą jednej lub dwóch opasek kablowych.
Upuść długopis w dwóch wywierconych otworach. Upewnij się, że wstrzykiwacz swobodnie przesuwa się w górę iw dół.
Przymocuj „kołnierz” do pióra w taki sposób, aby pióro było po prostu z dala od bębna, gdy serwo znajduje się w pozycji podnoszonej.
[1] Aluminium można ciąć, nacinając obie strony arkusza ostrym nożem (box-cutter), a następnie zaginając cięcie nad krawędzią stołu. Kilka ruchów i prześcieradło pęknie, pozostawiając prostą przerwę. W przeciwieństwie do nożyc do blachy ta metoda nie powoduje załamywania aluminium.
Krok 3: Bęben



Bęben składa się z odcinka rury z tworzywa sztucznego z dwoma drewnianymi zaślepkami [1].
Użyj cyrkla ustawionego na wewnętrzny promień rury, aby narysować kontury zaślepek końcowych. Teraz wytnij każdy kontur za pomocą cienkiej piły tarczowej („coping”, „fret”), a następnie dopasuj indywidualnie każdą zaślepkę za pomocą tarnika do drewna. Zamocuj zaślepki za pomocą małych wkrętów do drewna z łbem wpuszczanym.
Oś stanowi śruba inżynierska o średnicy 6 mm przechodząca przez środek każdej zaślepki końcowej.
Wymiary bębna
Wymiary bębna zależą od rozmiaru papieru. Średnica bębna 100 mm obsługuje formaty A4 w orientacji pionowej i A3 w orientacji poziomej. Średnica bębna 80 mm obsługuje tylko format A4 w orientacji poziomej. Użyj jak najmniejszej średnicy bębna, aby zmniejszyć bezwładność… silniki BYJ-48 są tylko małe.
Średnica bębna 90 mm jest idealna dla papieru A4 w orientacji pionowej i A3 w orientacji poziomej, ponieważ przeciwległe krawędzie po owinięciu wokół bębna zachodzą na siebie na około 10 mm, co oznacza, że wystarczy tylko jeden szew do przyklejenia.
Obracanie bębna
Każda oś przechodzi przez aluminiowy wspornik końcowy, dzięki czemu bęben może się swobodnie obracać. Pływanie końcowe zapobiega się za pomocą koła pasowego GT-2, 20 zębów, otworu 6 mm, przymocowanego do osi z jednej strony. Ciągły pasek rozrządu GT-2 łączy motoreduktor krokowy BJY-48 z bębnem. Silnik wymaga koła pasowego o średnicy otworu 5mm.
[1] Plastikowe zaślepki końcowe są dostępne dla większości średnic rur, ale zostały odrzucone, ponieważ pasują na rurę, a nie wewnątrz, a tworzywo sztuczne ma tendencję do zginania. Prawdopodobnie byłyby w porządku, gdyby zamiast śrub zastosowano oś ciągłą… ale wtedy potrzebny jest jakiś sposób mocowania osi do zaślepek końcowych.
Krok 4: Wskazówki konstrukcyjne
Upewnij się, że pióro przesuwa się po środku bębna. Można to osiągnąć wycinając rogi z drewnianych podpór. Jeśli pisak nie znajduje się na środku, będzie miał tendencję do zsuwania się z boku bębna.
Dokładne wiercenie dwóch otworów na pisaki jest ważne. Jakiekolwiek chybotanie prowadnicy pisaka lub zespołu karetki spowoduje chybotanie wzdłuż osi X.
Nie dokręcaj zbyt mocno pasków rozrządu GT-2… po prostu muszą być napięte. Silniki krokowe BYJ-48 nie mają dużego momentu obrotowego.
Silniki krokowe BJY-48 często wykazują niewielkie luzy, które są nieznaczne wzdłuż osi X, ale są niepokojące, jeśli chodzi o oś Y. Powodem tego jest to, że jeden obrót silnika osi Y równa się jednemu obrotowi bębna, podczas gdy karetka wymaga wielu obrotów silnika osi X, aby przebyć długość bębna. Wszelkie luzy w osi Y można wyeliminować, utrzymując stały moment obrotowy na bębnie. Prostą metodą jest przymocowanie niewielkiego ciężarka do nylonowej linki owiniętej wokół bębna.
Krok 5: Algorytm rysowania linii Bresenhama
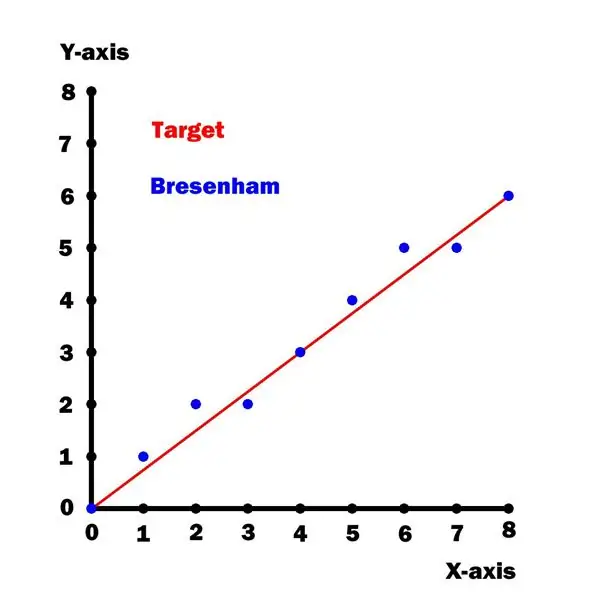
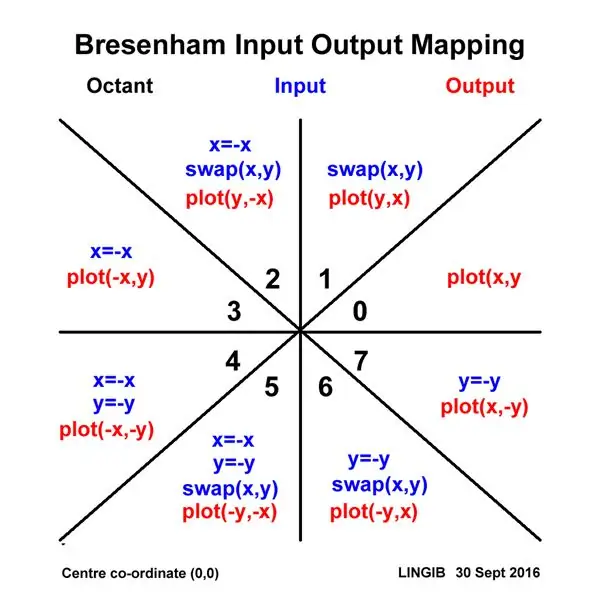
Ten ploter wykorzystuje zoptymalizowaną wersję [1] algorytmu rysowania linii Bresenhama. Niestety ten algorytm jest poprawny tylko dla nachyleń linii mniejszych lub równych 45 stopniom (tj. jeden oktant koła).
Aby obejść to ograniczenie, „mapuję” wszystkie wejścia XY do pierwszego „oktantu”, a następnie „odmapowuję” je, gdy nadejdzie czas na kreślenie. Funkcje mapowania wejść i wyjść, które to umożliwiają, są pokazane na powyższym schemacie.
Pochodzenie
Pozostała część tego kroku może zostać pominięta, jeśli znasz algorytm Bresenhama.
Narysujmy prostą od (0, 0) do (x1, y1) gdzie:
- x1=8=odległość w poziomie
- y1=6=odległość pionowa
Równanie dla linii prostej przechodzącej przez początek układu współrzędnych (0, 0) dane jest równaniem y=m*x gdzie:
m=y1/x1=6/8=0,75=nachylenie
Prosty algorytm
Prosty algorytm wykreślania tej linii to:
- int x1=8;
- int y1=6;
- pływak m=y1/x1;
- działka (0, 0);
- for (int x=1; x<=x1; x++) {
- int y=okrągły(m*x);
- działka(x, y);
- }
Tabela 1: Prosty algorytm
| x | m | m*x | tak |
|---|---|---|---|
| 0 | 0.75 | 0 | 0 |
| 1 | 0.75 | 0.75 | 1 |
| 2 | 0.75 | 1.5 | 2 |
| 3 | 0.75 | 2.25 | 2 |
| 4 | 0.75 | 3 | 3 |
| 5 | 0.75 | 3.75 | 4 |
| 6 | 0.75 | 4.5 | 5 |
| 7 | 0.75 | 5.25 | 5 |
| 8 | 0.75 | 6 | 6 |
Z tym prostym algorytmem wiążą się dwa problemy:
- główna pętla zawiera mnożenie, które jest powolne
- używa liczb zmiennoprzecinkowych, które również są wolne
Wykres y w funkcji x dla tej linii pokazano powyżej.
Algorytm Bresenhama
Bresenham wprowadził koncepcję terminu błędu „e”, który jest inicjowany na zero. Zdał sobie sprawę, że wartości m*x pokazane w tabeli 1 można uzyskać przez kolejne dodawanie „m” do „e”. Następnie zdał sobie sprawę, że y jest zwiększane tylko wtedy, gdy część ułamkowa m*x jest większa niż 0,5. Aby utrzymać porównanie w zakresie 0<=0,5<=1, odejmuje 1 od 'e' za każdym razem, gdy y jest zwiększane.
- int x1=8;
- int y1=6;
- pływak m=y1/x1;
- int y=0;
- pływak e=0;
- działka (0, 0);
- for (int x=1; x<=x1; x++) {
- e+= m;
- jeśli (e>= 0,5) {
- e-= 1;
- y++;
- }
- działka(x, y);
- }
Tabela 2: Algorytm Bresenhama
| x | m | mi | e-1 | tak |
|---|---|---|---|---|
| 0 | 0.75 | 0 | 0 | 0 |
| 1 | 0.75 | 0.75 | -0.25 | 1 |
| 2 | 0.75 | 0.5 | -0.5 | 2 |
| 3 | 0.75 | 0.25 | 2 | |
| 4 | 0.75 | 1 | 0 | 3 |
| 5 | 0.75 | 0.75 | -0.25 | 4 |
| 6 | 0.75 | 0.5 | -0.5 | 5 |
| 7 | 0.75 | 0.25 | 5 | |
| 8 | 0.75 | 1 | 0 | 6 |
Jeśli przyjrzysz się algorytmowi i tabeli 2, zauważysz to;
- główna pętla wykorzystuje tylko dodawanie i odejmowanie… nie ma mnożenia
- wzór dla y jest taki sam jak dla tabeli 1.
Ale nadal używamy liczb zmiennoprzecinkowych… naprawmy to.
Algorytm Bresenhama (zoptymalizowany)
Algorytm zmiennoprzecinkowy Bresenhama można przekonwertować na postać całkowitą, jeśli przeskalujemy 'm' i 'e' o 2*x1, w którym to przypadku m=(y1/x1)*2*x1=2*y1
Oprócz skalowania 'm' i 'e' algorytm jest podobny do powyższego z wyjątkiem:
- dodajemy 2*y1 do 'e' za każdym razem, gdy zwiększamy 'x'
- zwiększamy y, jeśli e jest równe lub większe niż x1.
- odejmujemy 2*x1 od 'e' zamiast 1
- Do porównania używa się x1 zamiast 0,5
Szybkość algorytmu można dodatkowo zwiększyć, jeśli pętla wykorzystuje zero do testu. Aby to zrobić, musimy dodać przesunięcie do terminu błędu 'e'.
- int x1=8;
- int y1=6;
- int m=(y1<<1); //stała: nachylenie przeskalowane o 2*x1
- int E=(x1<<1); //stała: 2*x1 do użycia w pętli
- int e = -x1; //przesunięcie -E/2: test teraz wykonany na zero
- działka (0, 0);
- int y=0;
- dla (x=1; x<=x1; x++) {
- e += m;
- jeśli (e>=x1) {
- e -= E
- y++;
- }
- działka(x, y);
- }
Tabela 3: Algorytm Bresenhama (zoptymalizowany)
| x | m | mi | mi | e - E | tak |
|---|---|---|---|---|---|
| 0 | 12 | 16 | -8 | 0 | |
| 1 | 12 | 16 | 4 | -12 | 1 |
| 2 | 12 | 16 | 0 | -16 | 2 |
| 3 | 12 | 16 | -4 | 2 | |
| 4 | 12 | 16 | 8 | -8 | 3 |
| 5 | 12 | 16 | 4 | -12 | 4 |
| 6 | 12 | 16 | 0 | -16 | 5 |
| 7 | 12 | 16 | -4 | 5 | |
| 8 | 12 | 16 | 8 | -8 | 6 |
Ponownie wzór dla y jest taki sam jak w innych tabelach. Warto zauważyć, że tabela 3 zawiera tylko liczby całkowite i że stosunek m/E=12/16=0,75, który jest nachyleniem „m” linii.
Ten algorytm jest niezwykle szybki, ponieważ główna pętla obejmuje tylko dodawanie, odejmowanie i porównywanie z zerem. Mnożenie nie jest używane, z wyjątkiem sytuacji, gdy inicjujemy wartości „E” i „m” za pomocą „przesunięcie w lewo”, aby podwoić wartości x1 i y1.
[1] Ta zoptymalizowana wersja algorytmu Bresenhama pochodzi z artykułu "Bresenham Line and Circle Drawing", copyright © 1994-2006, W Randolph Franklin (WRF). Jego materiały mogą być wykorzystywane do badań i edukacji non-profit, pod warunkiem, że je uznasz i zamieścisz link do jego strony głównej,
Krok 6: Kodeks
Pobierz załączony plik do folderu o tej samej nazwie, a następnie prześlij go do plotera za pomocą arduino IDE (zintegrowane środowisko programistyczne).
Odłącz moduł bluetoorh HC-06 przed próbą wgrania. Jest to konieczne, aby uniknąć konfliktu portu szeregowego z kablem USB.
Kod strony trzeciej
Oprócz powyższego kodu.ino będziesz potrzebować następujących pakietów oprogramowania, które są bezpłatne / dotacje:
- Teraterm, który jest dostępny pod adresem
- Inkscape, który jest dostępny na
Instrukcje dotyczące instalacji i używania każdego z powyższych pakietów stron trzecich można znaleźć w moim artykule
Krok 7: Menu
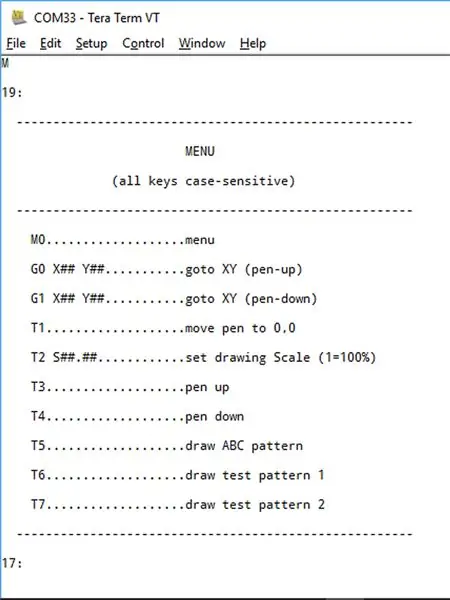
Nawiąż połączenie bluetooth z ploterem za pomocą "Teraterm".
Włącz „caps lock”, ponieważ wszystkie polecenia są pisane wielkimi literami.
Wpisz literę „M”, a powinno pojawić się menu, jak pokazano powyżej.
Menu jest dość oczywiste:
- M (lub M0) wywołuje menu
- G0 pozwala na wysłanie pisaka do określonej współrzędnej XY z podniesionym pisakiem.
- G1 umożliwia wysłanie pisaka do określonej współrzędnej XY z opuszczonym pisakiem.
- T1 umożliwia umieszczenie pióra nad współrzędną 0, 0. Wpisz „E”, aby wyjść.
- T2 pozwala na skalowanie rysunku. Na przykład "T2 S2.5" przeskaluje twój rysunek 250%. Domyślna skala to 100%
- T3 i T4 umożliwiają podnoszenie lub opuszczanie pióra.
- T5 rysuje wzór testowy „ABC”.
- T6 rysuje „cel”.
- T7 rysuje zestaw promieniowych linii, których celem jest sprawdzenie, czy algorytm Bresenhama działa w każdym z ośmiu „oktantów”
Uwagi:
- wszystkie ruchy pisaka używają skali rysunku ustawionej za pomocą opcji menu T2
- liczby „17:” i „19:” to kody uzgadniania terminala „Xon” i „Xoff” z interpretera arduino.
Krok 8: Kalibracja
Wartości X_STEPS_PER_MM i Y_STEPS_PER_MM dotyczą bębna o średnicy 90 mm.
Wartości dla innych średnic bębna można obliczyć z następujących zależności:
- obwód bębna to PI*średnica
- 2048 kroków to jeden obrót każdego wału silnika
- jeden obrót koła pasowego GT-2 odpowiada 40 milimetrowemu ruchowi liniowemu paska rozrządu
Inną metodą jest wprowadzenie następujących poleceń,
- G1 X0 Y100
- G1 X100 Y100
następnie zmierz długość otrzymanych linii i „przeskaluj” wartości X-STEPS_PER_MM i Y_STEPS_PER_MM
Krok 9: Wstępne przetwarzanie Gcode
Ten ploter wymaga tylko czterech gkodów Inkscape (mianowicie: G0, G1, G2, G3). Kod będzie działał znacznie szybciej, jeśli usuniemy wszystkie niepotrzebne gcode i komentarze.
Aby to zrobić, potrzebujesz kopii "Notepad++". Ten darmowy edytor tekstu zawiera wyszukiwarkę "wyrażeń regularnych" do znajdowania i usuwania niechcianego tekstu. Notepad ++ jest dostępny na
Otwórz plik do modyfikacji za pomocą Notepad ++ i umieść kursor na górze pliku.
Wybierz „Wyświetl/pokaż symbol/wszystkie znaki”, a następnie „Wyszukaj/zamień…” z górnego paska menu.
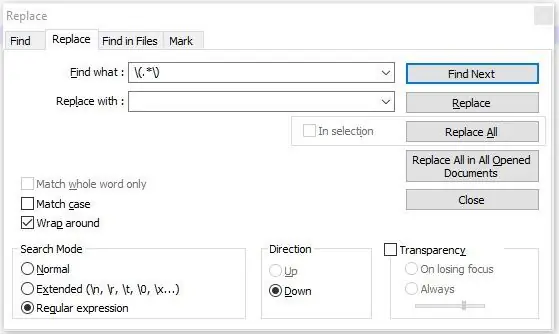
Kliknij pole wyboru „Wyrażenie regularne” (patrz pierwszy obraz) i wprowadź każdą z następujących sekwencji kodu w polu wyszukiwania.
Kliknij „Zamień wszystko” po każdym wpisie:
- %
- (.*)
- ^M.*$
- Z.*$
Powyższe wyrażenia regularne usuwają wszystkie symbole %, wszystkie komentarze pokazane w nawiasach, wszystkie kody M, wszystkie kody Z i kody, które następują.
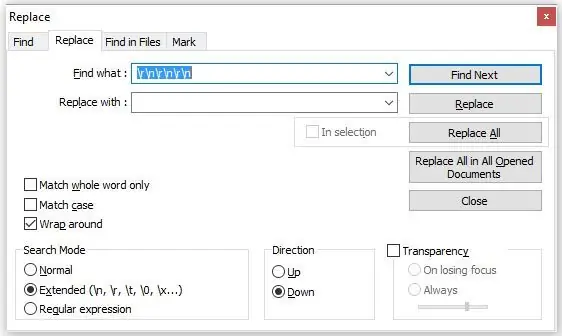
Teraz kliknij pole wyboru „Extended Expression” (patrz drugi obraz) i wprowadź następującą sekwencję kodu:
r\n\r\n\r\n
To wyrażenie usuwa niechciane powrót karetki i znaki wysuwu wiersza utworzone przez pierwszą sekwencję.
Zapisz plik pod inną nazwą, używając opcji „Zapisz jako”.
Gotowe.
Krok 10: Wyniki

Ten ploter został zbudowany jako „proof of concept” i nigdy nie miał być doskonały. Powiedziawszy, że wyniki nie są takie złe. Zdecydowanie spełniają mój cel projektowy polegający na przeniesieniu konturów akwareli na papier.
Pierwsze trzy obrazy to wbudowane wzorce testowe odpowiednio T5, T6, T7.
„Witaj świecie!” wzór został wysłany do plotera przez bluetooth. Załączona jest „wstępnie przetworzona” kopia tego pliku.
Krok 11: Aktualizacja kodu
Kod tego plotera został zaktualizowany do Drum_Plotter_V2.ino.
Zmiany w stosunku do oryginalnego Drum_Plotter.ino obejmują:
- płynniejsze pozycjonowanie pióra
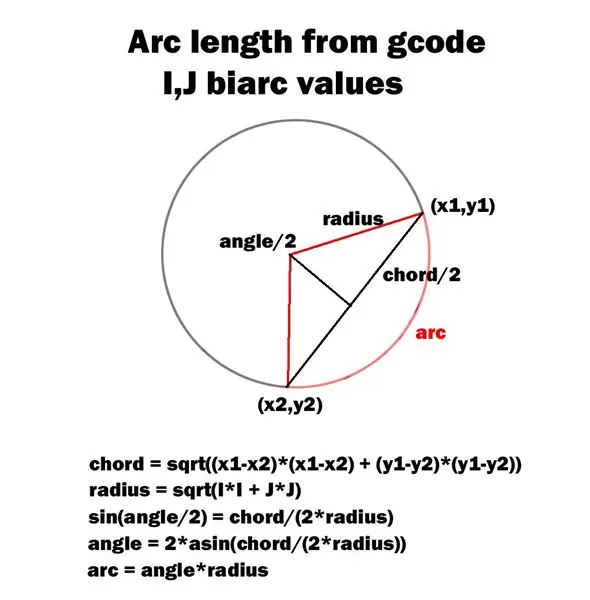
- teraz rozpoznaje instrukcje gcode G02 (zgodnie z ruchem wskazówek zegara)
- teraz rozpoznaje instrukcje gcode G03 (łuki w kierunku przeciwnym do ruchu wskazówek zegara)
Załączony schemat przedstawia moją metodę obliczania kąta łuku.
Krok 12: Drum_plotter_v3.ino
Załączono aktualizację kodu dla "CNC Drum Plotter".
"drum_plotter_v3.ino" naprawia drobny błąd, który wpływał na dokładność plotera.
Zmieniać historię
Wersja 2:
Dodano krzywe dwułukowe
Wersja 3:
Poniższe funkcje zostały przepisane w celu usunięcia drobnego błędu, który wpłynął na dokładność plotera.
- (int) zastąpione przez round() w funkcji move_to().
- Funkcja draw_line() „Oktant” poprawiony algorytm wyszukiwania
- Interpreter używa teraz funkcji ciągów zamiast wskaźników, co upraszcza projekt. Na przykład możemy teraz wyszukać „MENU”, zamiast szukać litery „M”, a następnie wyodrębnić następującą liczbę całkowitą. Pozwala to na personalizację plotera za pomocą własnych poleceń.
Krok 13: Drum_plotter_plotter_v4.ino
16 stycznia 2017:
Kod tego plotera bębnowego został dodatkowo zoptymalizowany. Dodano dodatkowe funkcje.
Zmiany obejmują:
- szybszy algorytm draw_line()
- dopasowanie funkcji move_to()
- liczniki kroków
- drobna poprawka błędu
Aby uzyskać więcej informacji, przeczytaj komentarze w załączonym "drum_plotter_v4.ino".
Kliknij tutaj, aby wyświetlić inne moje instrukcje.
Zalecana:
OBROTOWY PLOTER BUTELEK CNC: 9 kroków (ze zdjęciami)

Ploter ROTACYJNY DO BUTELEK CNC: Wziąłem kilka rolek, które prawdopodobnie są używane w drukarce. Wpadłem na pomysł, aby zamienić je w oś obrotu plotera do butelek CNC. Dzisiaj chciałbym się podzielić jak zbudować ploter do butelek CNC z tych rolek i innych skrawków.Aby d
Ploter robota CNC: 11 kroków (ze zdjęciami)

Ploter robota CNC: a.articles {font-size: 110,0%; grubość czcionki: pogrubiona; styl czcionki: kursywa; dekoracja tekstu: brak; background-color: red;} a.articles:hover {background-color: black;} Ta instrukcja opisuje sterowany CNC ploter robota. Robot składa się z
Ploter CNC Arduino (MASZYNA DO RYSUNKÓW): 10 kroków (ze zdjęciami)

Ploter CNC Arduino (MASZYNA DO RYSOWANIA): Hej chłopaki! Mam nadzieję, że podobał Ci się mój poprzedni instruktaż „Jak stworzyć własną platformę szkoleniową Arduino” i jesteś gotowy na nowy, jak zwykle zrobiłem ten samouczek, aby poprowadzić Cię krok po kroku, robiąc tego rodzaju super niesamowite
Ploter Arduino Mini CNC (z projektem Proteus i płytką drukowaną): 3 kroki (ze zdjęciami)

Arduino Mini CNC Plotter (z Proteus Project i PCB): Ten ploter arduino mini CNC lub XY może pisać i tworzyć projekty w zakresie 40x40mm. Tak, ten zakres jest krótki, ale to dobry początek, aby wskoczyć do świata arduino. [Dałem wszystko w tym projekcie, nawet PCB, Proteus File, Przykładowy projekt
3-osiowy ploter CNC - 60"x60"x5" - JunkBot: 5 kroków (ze zdjęciami)
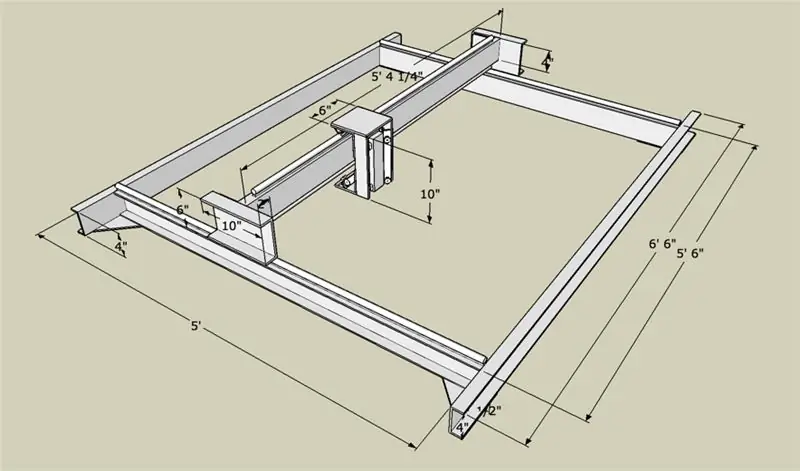
3-osiowy router CNC - 60"x60"x5" - JunkBot: Ten Instructable jest pierwszym z serii dokumentującej budowę 3-osiowego routera CNC DIY. Jest to również mój wpis do konkursu Universal Laser Cutter Contest.Cel tego Instructable nie jest pokazywanie pełnej progresji krok po kroku, ale raczej
