DIY Laserowy moduł sterujący dla Arduino: 14 kroków (ze zdjęciami)

2024 Autor: John Day | [email protected]. Ostatnio zmodyfikowany: 2024-01-30 11:32

W tym Instruktażu zademonstruję budowę dwuosiowego modułu sterującego wiązką laserową z jednym lustrem przy użyciu części drukowanych 3D i niedrogich komponentów z eBay.

Ten projekt ma podobieństwa do Arduino Laser Show z pełną kontrolą XY i Arduino Laser Show z Real Galvos, ale uważam, że jest to pierwszy projekt, który wykorzystuje druk 3D z niedrogimi solenoidami. Umieszczam wszystkie pliki projektowe na licencji GPLv3, aby projekt mógł zostać ulepszony i ulepszony.

Chociaż obecnie tylko zmontowałem moduł i napisałem bardzo prosty kod testowy, mam nadzieję, że pewnego dnia uda mi się przenieść go na wyższy poziom, włączając kod grafiki wektorowej z mojego wcześniejszego Instructable, Super Fast Analog Voltages z Arduino.

Krok 1: Zbierz części drukowane inne niż 3D

Zespół lasera składa się z następujących części:

• 4 mikro elektrozawory
• Jedno lustro 1/2 cala
• Cztery śruby M3

Poszczególne solenoidy, których użyłem, zostały zakupione w serwisie eBay za 1,45 USD za sztukę. Okrągłe lustro zostało znalezione w przejściu rzemieślniczym w HobbyLobby – paczka 25 sztuk kosztowała mnie mniej niż 3 dolary. Lustra można również znaleźć w serwisie eBay.

Będziesz także potrzebować niedrogiego wskaźnika laserowego z serwisu eBay. Fioletowy laser wraz ze świecącą w ciemności płytą winylową to doskonałe połączenie do tego projektu!

Zestaw pomocniczych dłoni nie jest konieczny, ale będzie bardzo przydatny do trzymania i pozycjonowania wskaźnika laserowego. Do przytrzymania przycisku zasilania można użyć dużego spinacza.

Będziesz potrzebował Arduino (ja użyłem Arduino Nano) i sposobu na napędzanie elektrozaworów. Jak stwierdził VajkF w komentarzach, możesz użyć gotowego mostka H, takiego jak te oparte na L298 lub L9110. Są one łatwo dostępne w serwisie eBay za kilka dolców i mogą być również używane do napędzania silników i projektów robotyki.

Ponieważ nie miałem mostka H, zbudowałem własny sterownik z elementów dyskretnych:

• Cztery tranzystory bipolarne NPN (użyłem MPS3704)
• Cztery rezystory (użyłem rezystora 1,2 kΩ)
• Cztery diody (użyłem 1N4004)
• Bateria 9V i złącze baterii

Elementy elektroniczne pochodziły z mojego laboratorium, więc nie mam za nie dokładnej ceny, ale o ile nie masz już części lub nie możesz ich usunąć, prawdopodobnie bardziej opłacalne jest użycie gotowego mostka H. Niemniej jednak dostarczę schematy do zbudowania własnego.

Krok 2: Wydrukuj w 3D lustrzany moduł sterujący

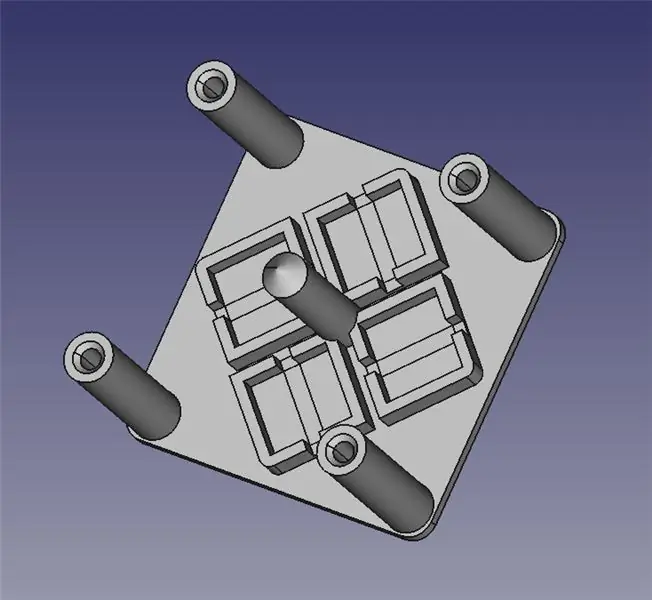
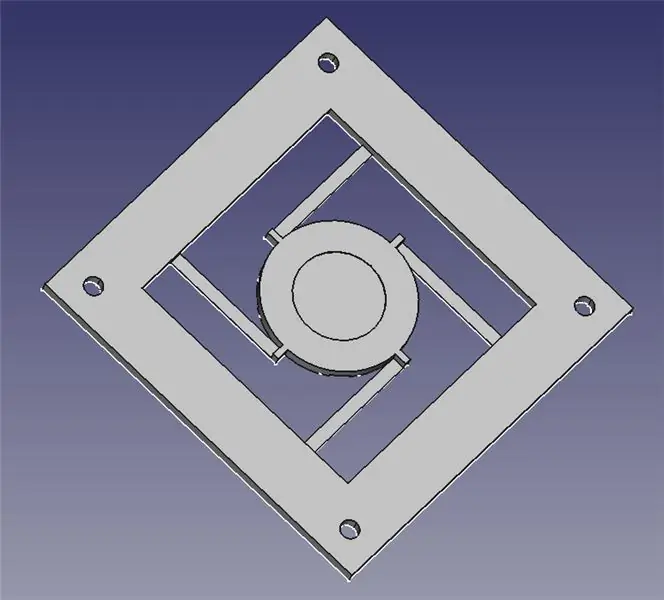
Laserowy moduł sterujący składa się z dwóch wydrukowanych w 3D części: podstawy do montażu czterech elektrozaworów oraz przegubowej platformy do lustra.

Załączam dwa pliki STL do druku 3D, a także pliki FreeCAD na wypadek konieczności modyfikacji projektu. Cała zawartość jest objęta licencją GPLv3, więc możesz swobodnie wprowadzać i udostępniać swoje ulepszenia!

Krok 3: Złóż moduł laserowy

• Użyj gorącego kleju, aby przymocować cztery solenoidy do dolnej części.
• Użyj gorącego kleju, aby przymocować lustro na środku górnej części.
• Włóż metalowe tłoki do elektrozaworów, a następnie umieść górną część na słupkach (ale nie przykręcaj jej). Lekko obróć górną część i za pomocą małego śrubokręta podnieś każdy tłok na miejsce. Krawędź tarczy powinna wsunąć się w rowek na tłoku. Uważaj, ponieważ zawiasy drukowane w 3D są bardzo delikatne. Przy cierpliwości i prawdopodobnie kilku nieudanych próbach powinieneś być w stanie ustawić wszystkie cztery tłoki bez skręcania lub naciskania na zawiasy.
• Po ustawieniu wszystkich tłoków częściowo włóż śruby M3, ale przed ich dokręceniem, delikatnie naciśnij każdy tłok i upewnij się, że lusterko swobodnie się przechyla. Jeśli nie porusza się swobodnie lub nie zahacza, może być konieczne zdjęcie górnej płyty, podważenie jednego lub więcej elektrozaworów i ponowne przymocowanie go pod niewielkim kątem na zewnątrz (może w tym pomóc umieszczenie podkładek dystansowych między nim a słupkiem środkowym).

Krok 4: Wydrukuj kołnierz wskaźnika laserowego

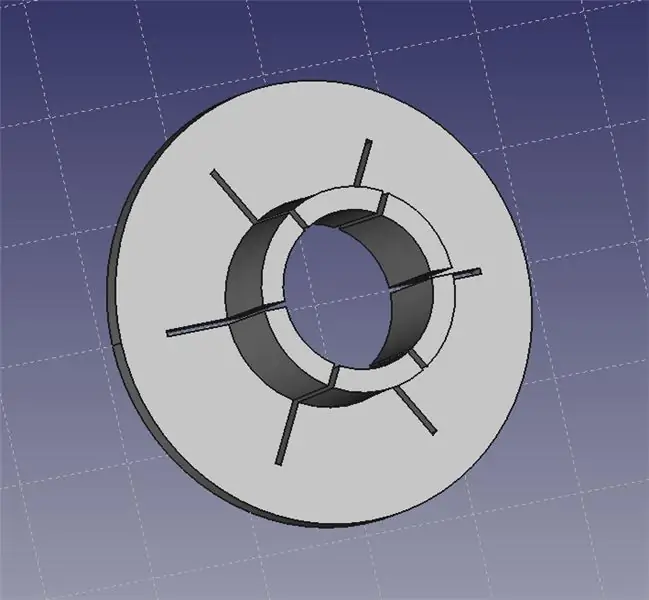
Kołnierz wskaźnika laserowego jest dopasowany do głowicy wskaźnika laserowego. Następnie możesz użyć zestawu pomocnych dłoni do uchwycenia kołnierza i umożliwienia precyzyjnego ustawienia lasera na ławce.

Krok 5: Złóż obwód napędowy

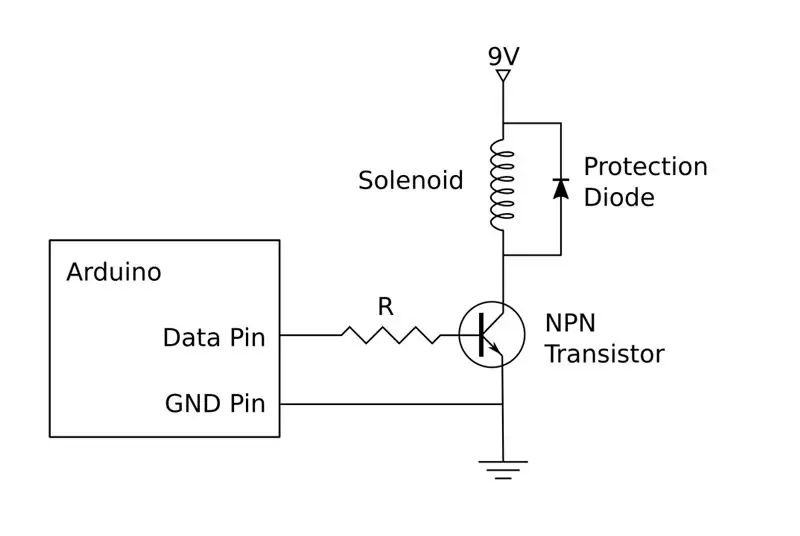
Obwód napędowy pokazano na schemacie. Jak wspomniano wcześniej, moja wersja jest zbudowana z elementów dyskretnych, ale można również użyć łatwo dostępnego mostka H. Jeśli zdecydujesz się zbudować własny, będziesz musiał zbudować cztery kopie tego obwodu, po jednym dla każdego z czterech elektrozaworów.

Każdy obwód połączy się z pinem Arduino, dwa do sterowania lewym i prawym elektrozaworem, a dwa do elektrozaworów górnego i dolnego. Będą one musiały być podłączone do pinów obsługujących PWM, na przykład:

• Pin 9: Elektromagnes w górę
• Pin 3: w dół elektromagnetyczny
• Pin 11: lewy elektromagnes
• Pin 10: prawy elektromagnes

Pojedyncza bateria 9V może być używana do zasilania wszystkich czterech obwodów sterownika elektromagnetycznego lub można użyć zasilacza stacjonarnego. Arduino wyłączy się z zasilania USB i nie powinno być podłączone do dodatniej strony baterii 9V. Jednak ujemna strona baterii jest używana jako uziemienie i powinna być podłączona do styku GND na Arduino, a także do styków emitera na tranzystorach.

Krok 6: Prześlij przykładowy kod

Przykładowy kod został zaktualizowany o następujące funkcje:

• Reguluje częstotliwość PWM tak, aby mechanizm był prawie bezgłośny przy niskich prędkościach. Brzęczenie w Motion Test 1 całkowicie zniknęło!
• Dodaje jako równania napięciowe na podstawie artykułu Schimpfa w celu „linearyzacji” nieliniowej odpowiedzi elektrozaworów.

Dołączyłem również implementację Lorenz Attractor opartą na kodzie z tego bloga.

Wierność wyników pozostawia sporo do życzenia, ale wciąż nad tym pracuję!:)

Kolejne kroki ilustrują niektóre techniki użyte w kodzie.

Krok 7: Zmniejszanie głośności

W moim Motion Test 1 słychać głośne brzęczenie, szczególnie podczas ruchu w górę iw dół. Okazuje się, że było to spowodowane domyślną częstotliwością przerywania PWM Arduino w zakresie słyszalnym. Gwałtowne włączanie i wyłączanie napięcia cewki powodowałoby wibracje z tą częstotliwością, czyniąc z nich maleńkie głośniki.

Aby rozwiązać ten problem, zwiększyłem częstotliwość PWM w kodzie:

#define PWM_FREQ_31372Hz 0x01 // Ustawia częstotliwość PWM na 31372,55 Hz#define PWM_FREQ_3921Hz 0x02 // Ustawia częstotliwość PWM na 3921.16 Hz #define PWM_FREQ_980Hz 0x03 // Ustawia częstotliwość PWM na MTCRBimer = MTCRB & 0b11111000) | częstotliwość; // Ustaw częstotliwość timera1 (piny 9 i 10) TCCR2B = (TCCR2B i 0b11111000) | częstotliwość; // Ustaw częstotliwość timera2 (piny 3 i 11) }

Ustawienie częstotliwości PWM Arduino to przydatna sztuczka do wyciszania elektrozaworów lub silników. Eksperymentuj z różnymi opcjami częstotliwości, aby zobaczyć, która daje najlepsze wyniki. Chociaż wiąże się to z bardziej zaawansowanym programowaniem, dobre źródło informacji na temat działania liczników jest tutaj.

Krok 8: Dostrajanie napięć w celu zmniejszenia zniekształceń

Moje wstępne testy ruchu wykazały, że były to znaczne zniekształcenia w odpowiedzi elektrozaworów. W Motion Test 3 (rysunek po lewej) to, co miało być okrągłą spiralą, stało się prostokątną siecią o postrzępionych krawędziach.

Rozwiązanie tego problemu wymagało trochę matematyki, ale udało mi się znaleźć w sieci niesamowity artykuł, który pomógł mi zrozumieć problem na tyle dobrze, aby rozwiązać go w oprogramowaniu.

To, co następuje, prowadzi Cię przez proces, przez który przeszedłem, aby dostroić system i poprawić wygląd powstałych śladów!

Krok 9: Doskonalenie oprogramowania za pomocą matematyki

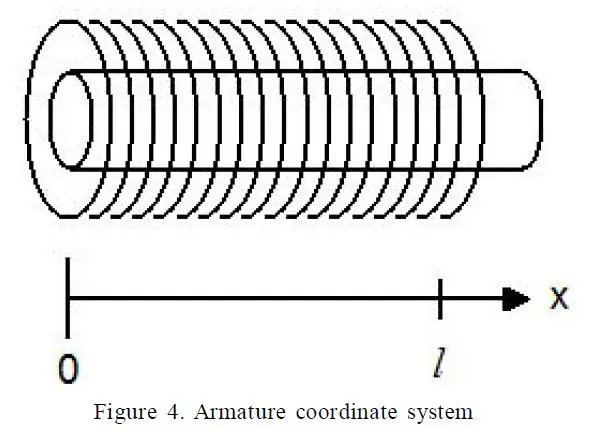
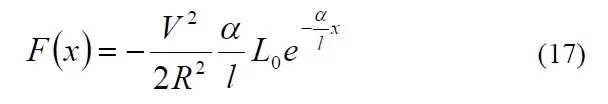
Sekretem dostrojenia systemu okazał się doskonały artykuł zatytułowany „Szczegółowe wyjaśnienie siły solenoidu” autorstwa Paula H. Schimpfa z Eastern Washington University (link). W szczególności równanie 17 dało mi siłę solenoidu w różnych kategoriach.

Następujące terminy były łatwe do zmierzenia:

• R - Opór mojego elektrozaworu
• l - Długość elektrozaworu
• x - Przemieszczenie tłoka w elektromagnesie
• V - Napięcie na elektromagnesie

Wiedziałem również, że siła wytworzona przez solenoid musi zrównoważyć siłę sprężyn drukowanych w 3D na lusterku dwuosiowym. Siła sprężyny podlega prawu Hooke'a, które brzmi następująco:

F = -kx

Chociaż nie znałem wartości k, przynajmniej wiedziałem, że siła, którą wyciągnąłem z równania 17 z pracy Schimpfa, musi być równa sile z prawa Hooke'a.

Wartość alfa (α) była trudna. Chociaż równania 13 i 14 pokazały, jak obliczyć te wartości z pola elektrozaworu (A), liczby zwojów (N) i wartości przenikalności magnetycznej (μ), nie chciałem rozrywać elektrozaworu, aby policzyć liczby zwojów, nie znałem też materiału, z którego wykonano rdzeń elektromagnesu.

Krok 10: Niedrogi tester komponentów ratuje dzień

Okazało się jednak, że równanie 15 i 16 dały mi to, czego potrzebowałem. Miałem niedrogi tester komponentów M328, który kupiłem w serwisie eBay za 10 USD. Był w stanie go użyć do pomiaru indukcyjności mojego solenoidu i odkryłem, że wpychanie zwory na różne głębokości daje mi różne wartości indukcyjne.

Pomiar z całkowicie włożoną zworą dał mi wartość L(0).

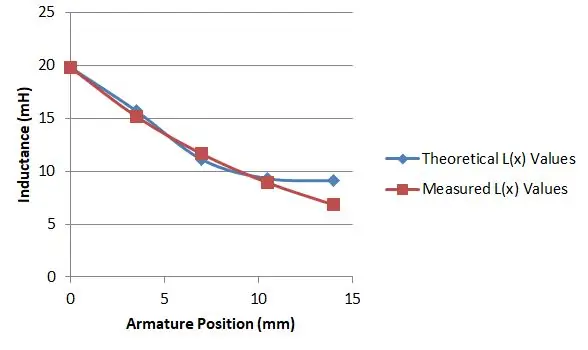
Długość mojego solenoidu wynosiła 14 mm, więc zmierzyłem indukcyjność z twornikiem w pięciu pozycjach, co dało mi różne wartości dla L(x):

• L(0,0) = 19,8 mH
• L(3,5) = 17,7 mH
• L(7,0) = 11,1 mH
• L(10,5) = 9,3 mH
• L(14) = 9,1 mH

Następnie użyłem arkusza kalkulacyjnego, aby wykreślić moje wartości w stosunku do wartości równań 15 i 16, dla konkretnego wyboru μr, a następnie zmieniałem swój wybór, aż znalazłem dobre dopasowanie. Stało się to, gdy μr wynosił 2,9, jak pokazano na wykresie.

Krok 11: Znajdź stałą sprężyny K, rozwiąż problem

Jedyną pozostałą niewiadomą była K, stała sprężystości. Zmierzyłem to, przykładając 9V do jednego z elektrozaworów w moim zespole dwuosiowym i mierząc odległość, w której lustro zostało ściągnięte. Dzięki tym wartościom udało mi się rozwiązać równania dla K, które znalazłem około 10,41.

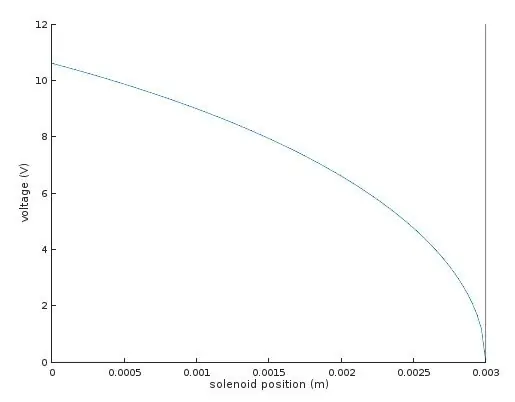
Miałem teraz wartości potrzebne do obliczenia ciągnięcia elektrozaworu w różnych pozycjach wzdłuż suwu. Ustawiając F(x) równą sile sprężyny z prawa Hooke'a, mogę obliczyć wymagane napięcie V.

Wykres pokazuje napięcie wymagane do przesunięcia elektrozaworu do dowolnej pozycji x.

Po prawej stronie, gdzie napięcie wynosi zero, a położenie 3 mm, odpowiada to neutralnemu punktowi spoczynku elektromagnesu, gdy zawiasy wydrukowane w 3D są całkowicie rozluźnione. Przesunięcie w lewo na wykresie odpowiada wciągnięciu zwory do solenoidu wbrew naciąganiu zawiasów wydrukowanych w 3D – początkowo wymaga to większego napięcia, ale gdy zwora wsuwa się głębiej w solenoid, przyciąganie wzrasta, a wymagane napięcie napędowe maleje.

Ta zależność jest zdecydowanie nieliniowa, ale dzięki równaniom z artykułu Schimpfa mogę napisać mój kod Arduino, aby wyprowadzał prawidłowe napięcia, aby ugięcie wiązki było liniowe:

float positionToVoltage(float x) {

// Przywrócenie siły wywieranej przez zawiasy (prawo Hooke'a) w żądanym x. const float sprężyna_F = -sprężyna_K * (x - sprężyna_X0); // Napięcie takie, że siła ciągnąca elektrozaworu odpowiada // sile przywracania zawiasów return sqrt(-2*R*R*(-spring_F)*solenoid_len/(a*L_0*exp(-a*x/solenoid_len))); }

Prowadzi to do znacznie bardziej okrągłej spirali niż w moim oryginalnym teście ruchu. Misja zakończona!

Krok 12: Pytania i odpowiedzi dotyczące obwodu sterownika wykorzystującego elementy dyskretne

Dlaczego nie mogę podłączyć elektrozaworu bezpośrednio do Arduino?

To kwestia tego, ile prądu może dostarczyć Arduino bez doznania uszkodzeń. To około 40mA na pin. Wiedząc, że Arduino pracuje pod napięciem 5V, możemy wykorzystać prawo Ohma do obliczenia wymaganej minimalnej rezystancji obciążenia (w tym przypadku elektrozaworu). Dzieląc 5 woltów przez 0,040 amperów, otrzymujemy 125 omów. Jeśli obciążenie ma większą rezystancję, możemy podłączyć je bezpośrednio do Arduino, w przeciwnym razie nie. Mały solenoid ma zazwyczaj rezystancję 50 omów, więc nie możemy go wysterować bezpośrednio z Arduino. Gdybyśmy to zrobili, pociągnąłby 100 mA, co jest zdecydowanie za dużo.

Dlaczego używasz 9V dla elektrozaworu, a 5V dla Arduino?

Arduino działa na 5V, ale to trochę za mało jak na solenoid. Użycie tranzystora pozwala nam wybrać napięcie dla solenoidu, które jest niezależne od 5V zastosowanego w Arduino.

Skąd mam wiedzieć, czy tranzystor nadaje się do tego projektu?

Podobnie jak w przypadku Arduino, głównym wymaganiem jest, aby prąd płynący przez solenoid nie przekraczał maksymalnych wartości znamionowych tranzystora (w szczególności prądu kolektora). Możemy łatwo obliczyć najgorszy scenariusz, mierząc rezystancję elektrozaworu, a następnie dzieląc przez to napięcie zasilania. W przypadku zasilania elektrozaworów 9V i rezystancji elektrozaworu 50 omów najgorszy scenariusz stawia nas na 180mA. Na przykład MPS3704 jest przystosowany do maksymalnego prądu kolektora 600 mA, co daje margines około 3.

Jak określić minimalną wartość rezystancji, jaką należy umieścić między wyjściem Arduino a bazą tranzystora?

Wyjście Arduino połączy podstawę tranzystorów bipolarnych poprzez rezystor ograniczający prąd. Ponieważ Arduino działa przy 5V, możemy ponownie użyć prawa Ohma do obliczenia rezystancji wymaganej do ograniczenia prądu poniżej 40mA. Oznacza to, że podziel 5 woltów przez 0,04 ampera, aby uzyskać wartość co najmniej 125 omów. Wyższe wartości rezystorów zmniejszą prąd, dając nam jeszcze większy margines bezpieczeństwa.

Czy istnieje maksymalna wartość tego oporu, której nie powinienem przekraczać?

Okazuje się, że tak. Tranzystor ma tak zwane wzmocnienie prądowe. Na przykład, jeśli wzmocnienie wynosi 100, oznacza to, że jeśli włożymy 1mA do bazy, to do 100mA popłynie przez obciążenie, którym steruje tranzystor. Jeśli włożymy 1,8mA do podstawy, to przez obciążenie popłynie do 180mA. Ponieważ wcześniej obliczyliśmy, że przy 9V przepływa 180mA przez elektrozawór, to prąd bazowy 1,8mA jest „sweet spot”, a mniej i nasz elektrozawór nie włączy się całkowicie.

Wiemy, że Arduino dostarcza 5 V i chcemy, aby płynął prąd 1,8 mA, więc używamy prawa Ohma (R=V/I) do obliczenia rezystancji (R=V/I). 5V podzielone przez 1,8mA daje rezystancję 2777 omów. Tak więc biorąc pod uwagę przyjęte przez nas założenia, spodziewamy się, że opór musi wynosić od 125 do 2777 – wybór około 1000 omów daje nam całkiem dobry margines bezpieczeństwa.

Krok 13: Analiza aktualnych problemów i możliwych rozwiązań

Obecny prototyp wykazuje potencjał, ale pozostaje kilka problemów:

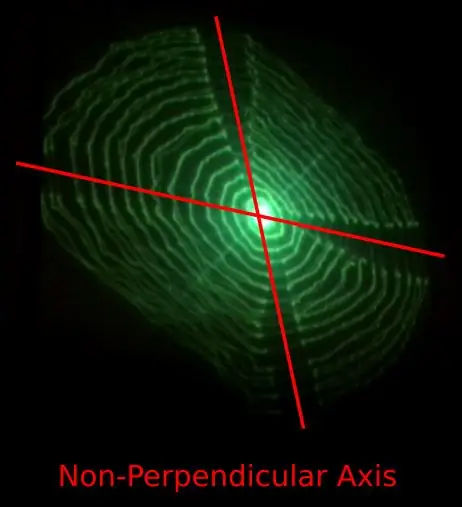
1. Ruch wzdłuż osi X i Y nie wydaje się być prostopadły.
2. Następuje przeskok, gdy lustro zmienia kierunek.
3. Rozdzielczość jest dość niska i widoczne są wzory stopni schodów.
4. Przy wyższych prędkościach ruchu ścieżka lasera jest zniekształcona przez wibracje i dzwonienie.

Problem 1) może być spowodowany konstrukcją wydrukowanych w 3D elastycznych zawiasów, które przenoszą ruch wzdłuż jednej osi do osi prostopadłej.

Problem 2) wynika z luzu w połączeniu między tłokami napędowymi a platformą lustra, co powoduje szarpanie lustra i przeskakiwanie przy przejściach między osiami X i Y. Ten nagły ruch prowadzi do zaciemnienia szczeliny w kształcie litery X, w której punkt lasera wykonuje szybszy niekontrolowany ruch.

Problem 3) występuje, ponieważ domyślny Arduino PWM ma tylko 255 poziomów, a sporo z nich jest marnowanych ze względu na kształt krzywej napięcia. Można to znacznie poprawić dzięki zastosowaniu timera1, który jest 16-bitowy i może obsługiwać 65536 unikalnych wartości.

Problem 4) występuje, ponieważ zwierciadło i przesuwna zwora elektromagnesu (tłoki) stanowią znaczną ilość poruszającej się masy.

Ponieważ kwestie 1) i 2) są związane z konstrukcją mechaniczną, jedną z możliwości może być usunięcie metalowych tłoków i zastąpienie ich małymi magnesami ziem rzadkich, które są przymocowane bezpośrednio do płyty przechylnej. Solenoidy byłyby otwartą cewką, która przyciągałaby lub odpychała magnesy bez fizycznego kontaktu. Doprowadziłoby to do płynniejszego ruchu i wyeliminowania możliwości szarpania przy jednoczesnym zmniejszeniu masy całkowitej.

Zmniejszenie masy jest podstawowym rozwiązaniem problemu 4), ale wszelkie pozostałe problemy można rozwiązać bezpośrednio w oprogramowaniu, wdrażając profil sterowania ruchem w oprogramowaniu, aby przyspieszać i zwalniać lustro w kontrolowany sposób. Jest to już powszechnie wykonywane w oprogramowaniu sprzętowym drukarki 3D i podobne metody mogą również działać tutaj. Oto kilka zasobów związanych ze sterowaniem ruchem w przypadku drukarek 3D:

• „Matematyka profili sterowania ruchem”, Chuck Lewin (link)
• „Objaśnienie ruchu kontrolowanego szarpnięciem”, (link)

Podejrzewam, że dodanie trapezoidalnego profilu kontroli ruchu pozwoliłoby na poruszanie lustra ze znacznie większymi prędkościami bez artefaktów dzwonienia lub wibracji.

Krok 14: Przyszła praca i możliwe zastosowania

Chociaż opracowanie rozwiązań tych problemów będzie wymagało sporo pracy, mam nadzieję, że ten moduł sterowania wiązką typu open source może stać się niedrogą alternatywą dla projektów opartych na galwanometrach w takich zastosowaniach, jak:

• Niedrogie pokazy laserowe dla DJ-ów i VJ-ów.
• Elektromechaniczny wyświetlacz wektorowy do klasycznej gry zręcznościowej, takiej jak Vectrex.
• Drukarka 3D typu SLA z żywicy DIY, która w duchu ruchu RepRap może drukować własny laserowy moduł sterujący.
• Cyfrowe panoramowanie lub optyczna stabilizacja obrazu w kamerach.

II nagroda w konkursie Arduino 2017