Czy wiesz o regulacji ADC ESP32?: 29 kroków

2024 Autor: John Day | [email protected]. Ostatnio zmodyfikowany: 2024-01-30 11:30

Dzisiaj opowiem o bardziej technicznym problemie, ale myślę, że każdy kto pracuje z ESP32 powinien wiedzieć: kwestia regulacji odczytu ADC (przetwornika analogowo-cyfrowego). Uważam to za ważne, ponieważ podczas „pomiaru”, zwłaszcza z instrumentem, który ma wyjście analogowe, musisz mieć absolutną pewność, że odczyt jest wykonywany prawidłowo.

W dzisiejszym filmie przeprowadzimy zatem pomiary za pomocą „przetwornika analogowo-cyfrowego” ESP32, zaobserwujemy rozbieżności konwersji i zastosujemy metodę regulacji/kalibracji ADC.

Krok 1: Co to jest konwerter AD?

Konwerter AD to obwód zdolny do przekształcania wielkości analogowej (ciągłej) na wartości cyfrowe (dyskretne). Co to znaczy? Oznacza to, że podczas gdy wartości cyfrowe mogą przyjmować tylko wartości dyskretne utworzone przez kombinację zer i jedynek, wielkość analogowa może przyjmować dowolną wartość w zakresie. Na przykład, gdybyśmy zmierzyli napięcie idealnego ogniwa AA, moglibyśmy znaleźć dowolną wartość między 0V a 1,5V, ponieważ jest to wielkość analogowa. Stan wyjściowy idealnej lampy musi przyjmować tylko dwa stany (wyłączony lub włączony), co jest wielkością dyskretną. Ponieważ mikrokontrolery działają przy użyciu tej dyskretnej logiki, potrzebujemy obwodu zdolnego do tłumaczenia wielkości analogowej na cyfrową (lub dyskretną).

Krok 2: Wykorzystane zasoby

• Jedna karta Lolin32 Lite v1.0.0

• Oscyloskop Tektronix TDS1001C do przechwytywania

• Jeden kabel USB do ESP32

• Oscyloskop Hantek DSO4102C jako generator sygnału

Krok 3: ADC ESP32

Według danych Espressif, układy ESP32 mogą wykazywać +/- 6% różnicę między układami w zmierzonych wynikach.

Ponadto konwersja NIE ma liniowej odpowiedzi dla każdego dostępnego zakresu do odczytu. Espressif zapewnia metodę kalibracji i sugeruje użytkownikom wdrożenie innych metod, jeśli uznają to za konieczne do osiągnięcia pożądanej dokładności.

Wykonamy akwizycję danych i na tej podstawie pokażemy odpowiedzi ADC oraz przykład zastosowania procesu matematycznego do odczytania korekty.

Istnieje kilka (prostszych lub bardziej złożonych) sposobów wykonania tych poprawek. To do Ciebie należy ocena najbardziej odpowiedniego dla Twojego projektu.

Ten pokazany tutaj będzie miał cel ilustracyjny i spróbuje zająć się interesującymi punktami, które można zaobserwować podczas korekt.

Krok 4: Użyty obwód

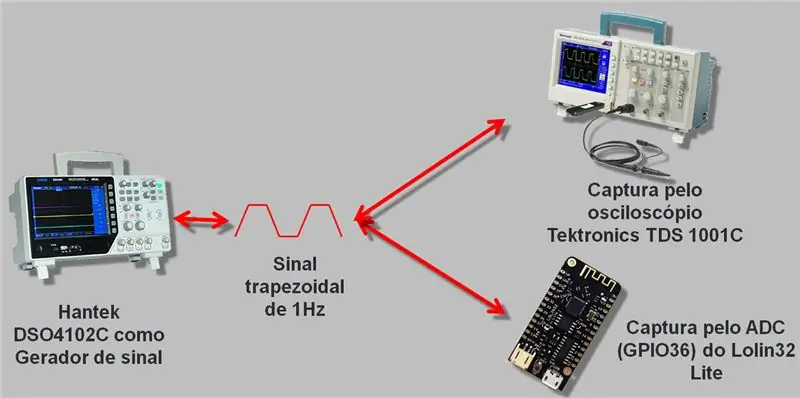
Użyłem oscyloskopu z generatorem sygnału, który dochodzi do 25 MHz, Hantek DSO4102C. Wygenerowaliśmy falę, która została odczytana przez ESP A/D i oscyloskop. Zebrane dane zostały zapisane w csv oraz w arkuszu kalkulacyjnym, który zostawię na końcu artykułu do pobrania.

Krok 5: Używany znak

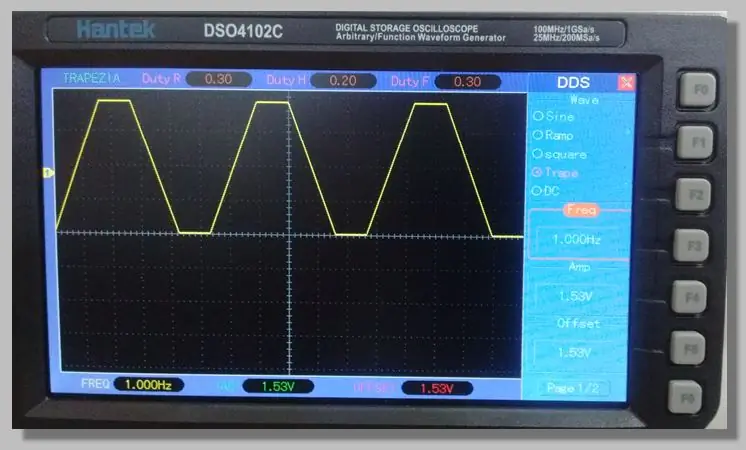
Wybraliśmy sygnał trapezowy o niskiej częstotliwości, który umożliwia dostęp do ramp przebiegających przez cały zakres konwersji. Pozwala to na dużą liczbę próbek na tych rampach.

Krok 6: Dane uzyskane przez oscyloskop

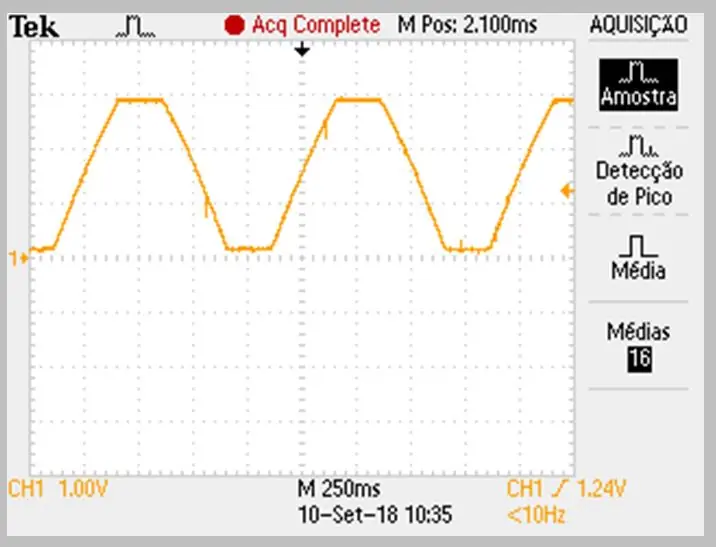
Obraz przechwytywania został wykonany przez oscyloskop. Dane zostały zapisane w pliku csv. Zwróć uwagę na delikatną krzywiznę na wznoszących się i opadających zboczach sygnału.

Krok 7: Dane uzyskane przez oscyloskop (plik csv w programie Excel)

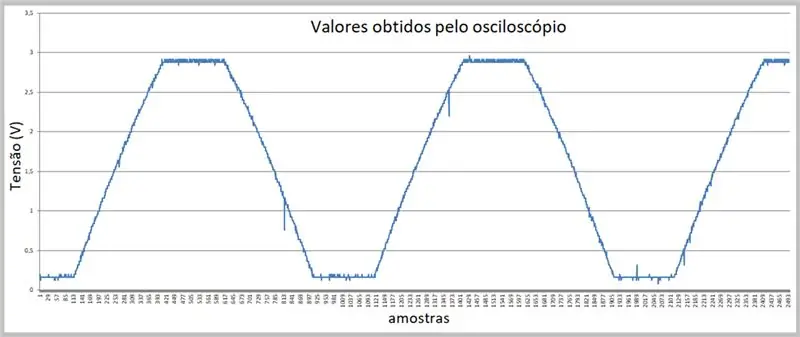
Mamy tutaj próbki.

Krok 8: Dane uzyskane przez ADC

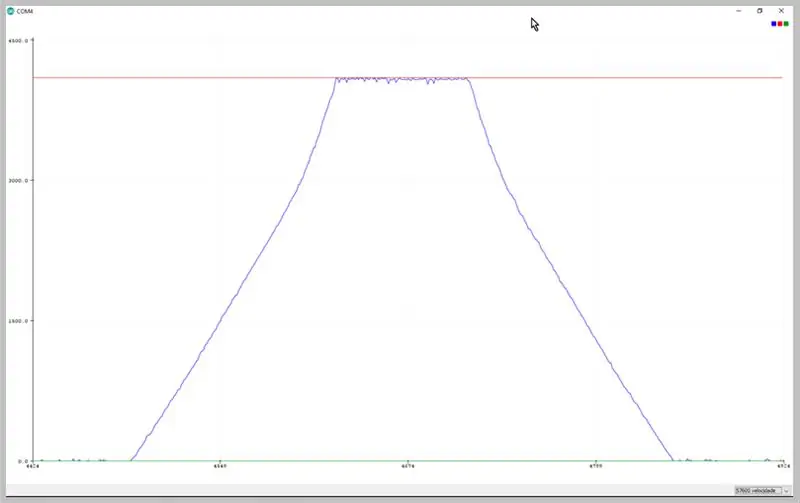
Zmieniając szybkość transmisji serialu, możemy przeglądać dane przechwycone przez ADC. Obserwuj deformację sygnału trapezowego.

Dane obserwowane na ploterze szeregowym Arduino IDE

Krok 9: Dane uzyskane przez ADC - Excel

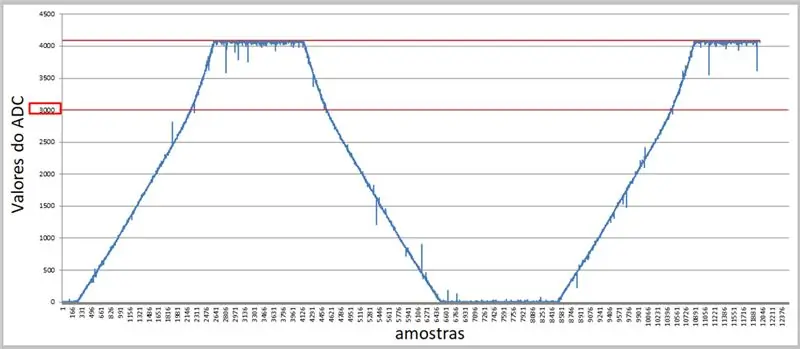
Używając wyższej szybkości i terminala szeregowego, możemy przechwycić wartości i zastosować je w Excelu do naszych porównań.

Krok 10: Porównanie ramp wznoszenia

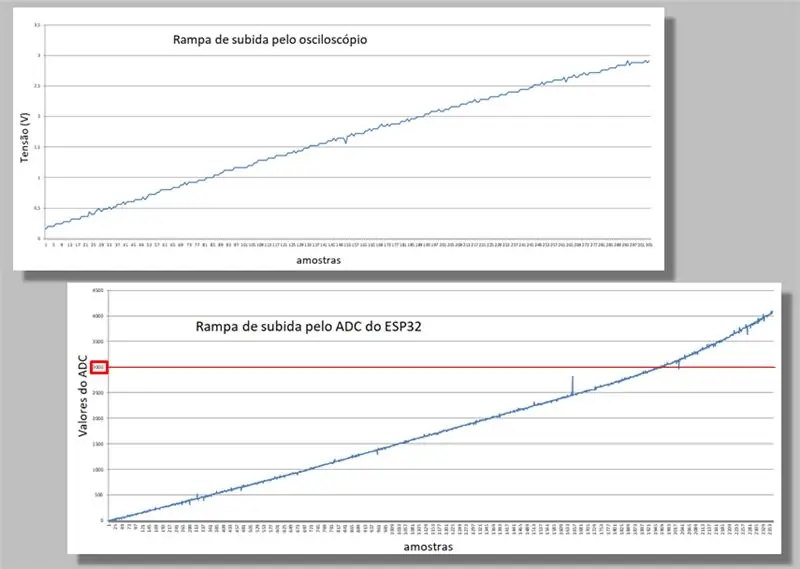
Porównujemy dwie rampy wspinaczkowe dwóch zaczepów.

Zwróć uwagę na krzywiznę występującą na obu rampach.

Zauważ też, że dla tej samej rampy mamy znacznie więcej próbek ESP32 niż z oscyloskopu.

Krok 11: Zrównanie liczby próbek

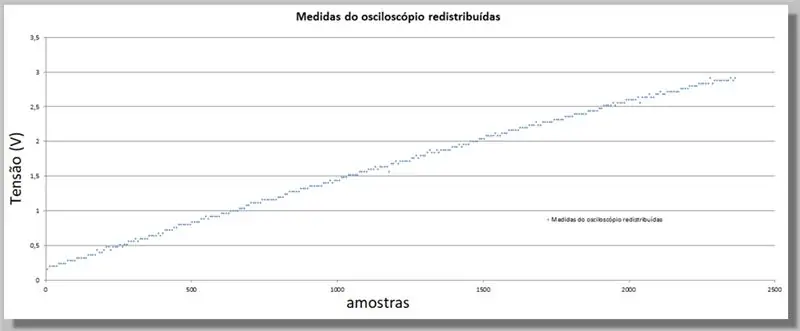
Ponieważ ESP32 dostarczył większą liczbę próbek niż oscyloskop, musimy zrównać te wartości, ponieważ będą one służyć jako wskaźnik do porównania obu krzywych.

W tym celu dokonamy bezpośredniego porównania.

Mamy 305 próbek na rampę oscyloskopową i 2365 próbek na rampę ADC.

Ponieważ rampy mają ten sam zakres, możemy powiedzieć, że mamy około 7,75 próbek ADC dla każdego oscyloskopu.

Mnożenie indeksu każdej próbki oscyloskopu ma tę samą krzywą, ale z indeksami odpowiadającymi ADC i redystrybuowanym danym.

Aby uzupełnić brakujące dane dla nowych pozycji, zastosujemy krzywą, która statystycznie pasuje do znanych danych.

Krok 12: Wypełnianie luk – linia trendu

Wybierając znane dane (niebieskie kropki), klikając a następnie prawym przyciskiem wybieramy: „Dodaj linię trendu…”

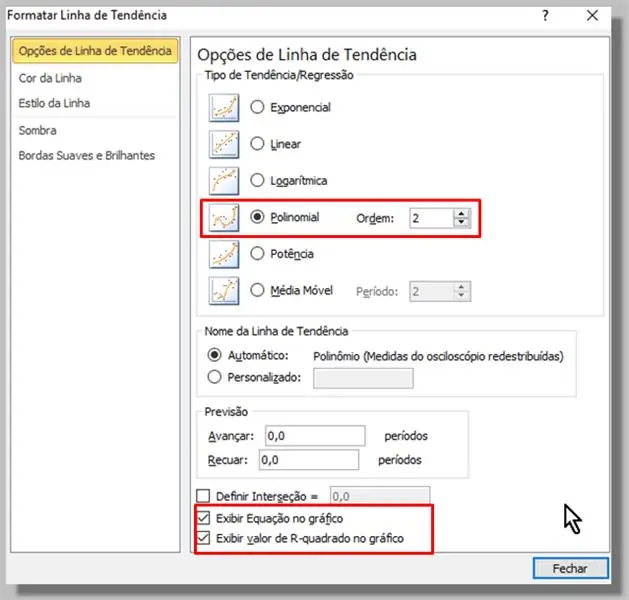
W wyświetlonym oknie wybieramy typ wielomianu (wystarczy kolejność 2).

Sprawdziliśmy również opcje „Wyświetl równanie na wykresie” i „Wyświetl wartość R-kwadrat na wykresie”.

Klikamy „Zamknij”.

Krok 13: Wypełnianie luk - krzywa wielomianu stopnia 2

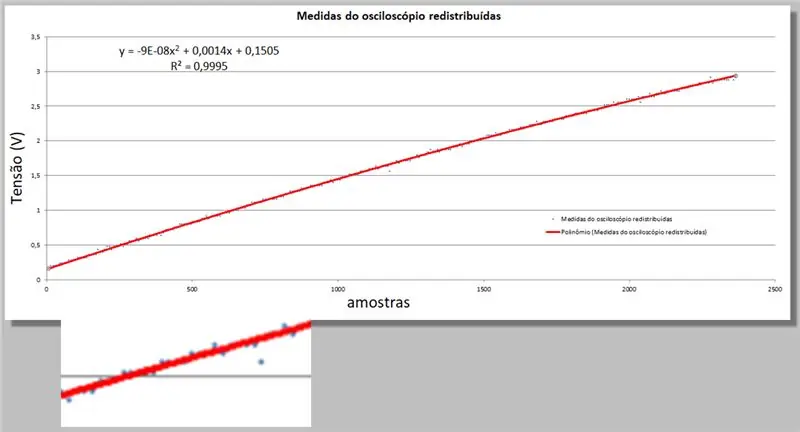
Excel daje nam dwie nowe informacje; równanie drugiego rzędu, które najlepiej pasuje do danych, oraz równanie R-kwadrat, które określa ilościowo tę adekwatność.

Pamiętaj tylko, że im bliżej 1, tym bardziej odpowiednie równanie.

Nie zagłębiajmy się w matematykę, po prostu użyjmy jej jako narzędzia.

Krok 14: Wypełnianie luk – ocena funkcji

Wypełnijmy luki w próbkowaniu danymi wygenerowanymi przez równanie. A następnie porównaj je punkt po punkcie.

y = -9E-08x2 + 0,0014x + 0, 1505

R² = 0, 9999

Napięcie oscyloskopu = -9E-08 * indeks2 + 0,0014 * indeks + 0,1505

Krok 15: Konwersja napięcia oscyloskopu na wartość równoważną w celu porównania z ADC

Wykorzystajmy to również do przekształcenia wartości napięcia oscyloskopu na równoważną wartość ADC.

Ponieważ najwyższa wartość uzyskana w ADP ESP32 wyniosła 4095, co odpowiada odczytowi 2,958V dla tego samego indeksu, możemy powiedzieć, że:

Każdy wolt w pomiarach oscyloskopu wynosi około 1384,4 jednostek AD. Dlatego wszystkie pomiary oscyloskopu możemy przemnożyć przez tę wartość.

Krok 16: Porównanie dwóch uzyskanych ramp

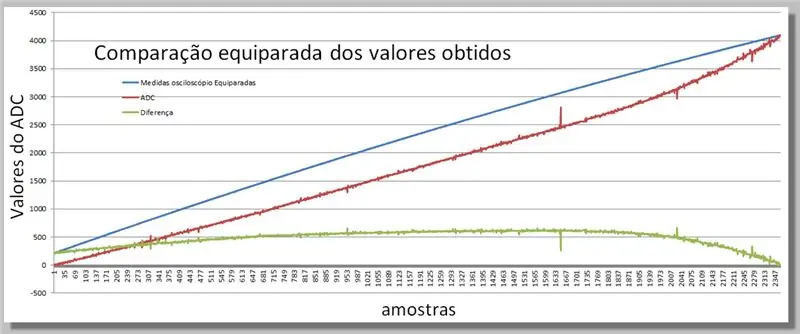
Wizualizacja różnic uzyskanych w dwóch odczytach.

Krok 17: Zachowanie różnicy odczytu ADC (BŁĄD)

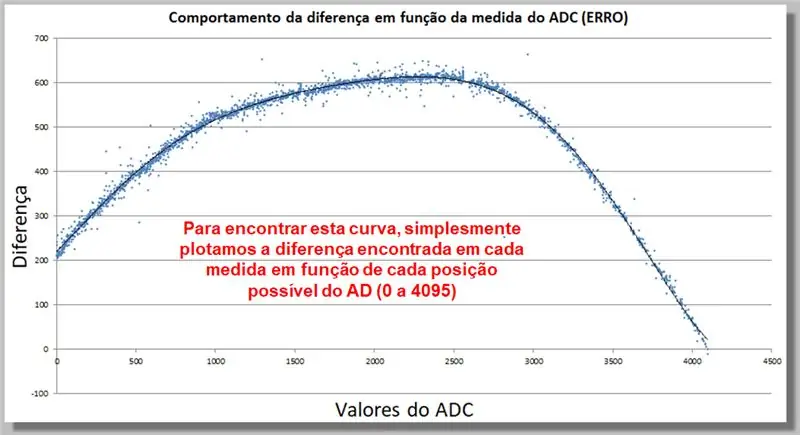
Poniższa krzywa pokazuje, jak zachowuje się różnica w odczycie ADC jako funkcja pomiaru. Ten zbiór danych pozwoli nam znaleźć funkcję korekty.

Aby znaleźć tę krzywą, po prostu wykreślamy różnicę znalezioną w każdej mierze jako funkcję każdej możliwej pozycji AD (od 0 do 4095).

Krok 18: Zachowanie ADC w zakresie odczytywania różnic - znajdowanie funkcji korekcji

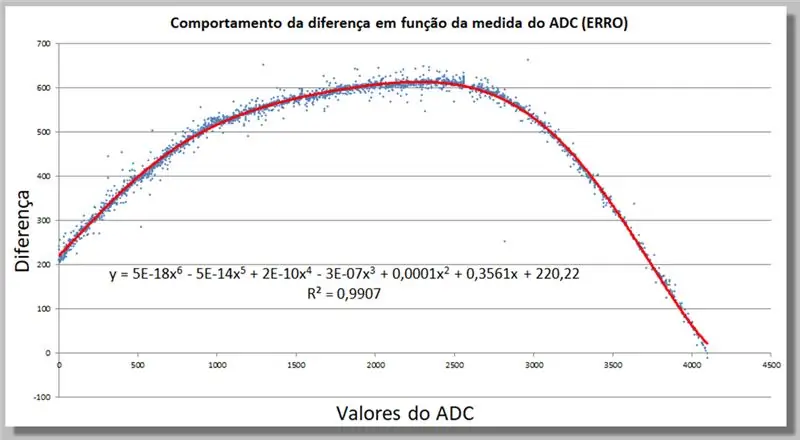
Możemy określić w Excelu funkcję korygującą, dodając linię trendu, teraz w wyższym stopniu, aż będzie wystarczająco dopasowana do naszych danych.

Krok 19: Korzystanie z innego oprogramowania

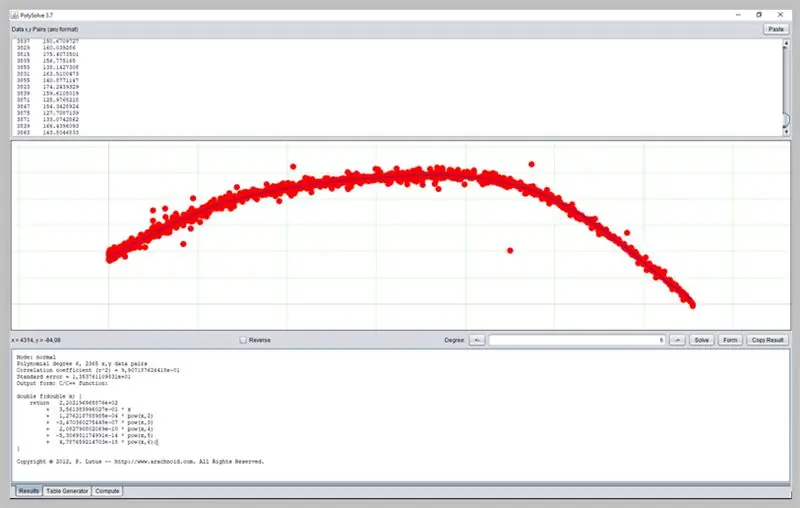
Innym ciekawym oprogramowaniem do wyznaczania krzywych jest PolySolve, które można wykorzystać bezpośrednio pod linkiem: https://arachnoid.com/polysolve/ lub pobrać jako aplikację Java.

Pozwala na zastosowanie regresji wielomianowych wyższego stopnia i dostarczenie sformatowanej funkcji, a także innych funkcjonalności.

Aby z niego skorzystać, wystarczy wpisać dane w pierwszym polu tekstowym. Dane muszą być uporządkowane w kolejności X, Y oddzielone przecinkiem lub tabulatorem. Zachowaj ostrożność przy prawidłowym używaniu kropki jako przecinka dziesiętnego.

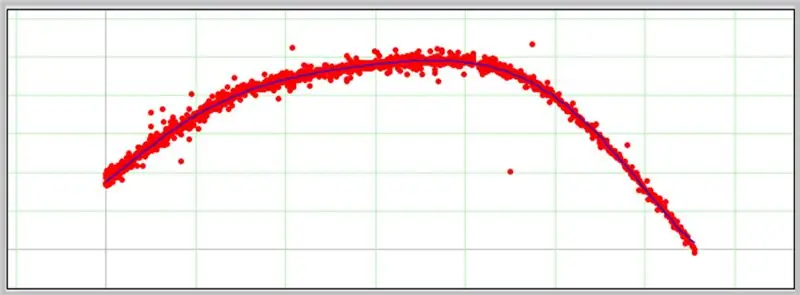
Wykres pojawi się w następnym polu, jeśli wprowadzone dane są poprawnie sformatowane.

Oto jak poszła nasza krzywa błędu ADC.

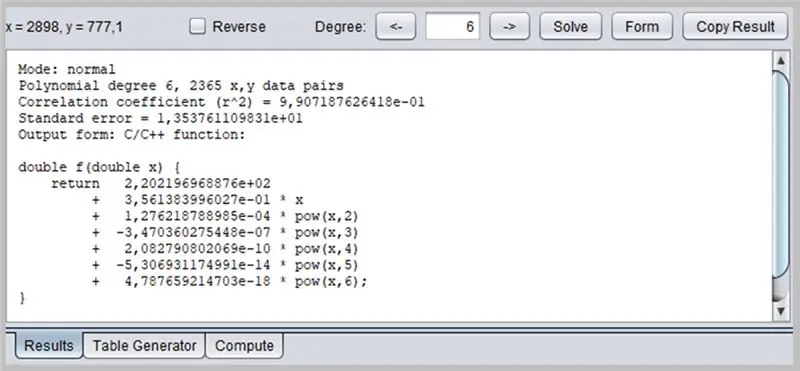
Okno to przedstawi wynik regresji, w tym dane adekwatności funkcji, które z kolei mogą mieć swoje dane wyjściowe sformatowane na kilka sposobów: jako funkcja C/C++, lista współczynników, funkcja napisana w Javie itp.

Uwaga: Zwróć uwagę na separatory dziesiętne

Krok 20: Stałe i konfiguracja ()

Wskazuję tutaj GPIO używane do przechwytywania analogowego. Inicjuję port szeregowy, a także pin wyznaczony do przechwytywania analogowego.

const int pin_leitura = 36; //GPIO usado para captura analógica void setup() { Serial.begin(1000000); //Zainicjuj port szeregowy do debugowania pinMode(pin_leitura, INPUT); //Pino utilizado para captura analógica }

Krok 21: Pętla () i funkcja korekcji

Przechwytujemy nastawione napięcie i drukujemy wartości z poprawnymi poprawkami lub bez nich.

void loop() { int valor_analogico = analogRead(pin_leitura); //realiza a captura da tensão ajustada //Serial.print(valor_analogico + f(valor_analogico)); //imprime os valores para debug (COM CORREÇÃO) Serial.print(valor_analogico); //imprimime os valores para debug (SEM CORREÇÃO) Serial.print(", "); Serial.print(4095);//cria uma linha para markar o valor máximo de 4095 Serial.print(", "); Serial.println(0); //cria uma linha para marcar o valor minimo de 0 }

Zauważ w linii 12, że mamy możliwość wydrukowania danych z dodatkiem funkcji różnicy f (wartość_analogowa).

Krok 22: Korzystanie z funkcji korekcji PolySolve

Tutaj używamy funkcji PolySolve wewnątrz Arduino IDE.

/* Tryb: normalny Stopień wielomianu 6, 2365 pary danych x, y Współczynnik korelacji (r^2) = 9, 907187626418e-01 Błąd standardowy = 1, 353761109831e+01 Forma wyjściowa: funkcja C/C++: Copyright © 2012, P. Lutus – https://www.arachnoid.com. Wszelkie prawa zastrzeżone. */ double f(double x) { return 2.202196968876e+02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow(x, 2) + -3.470360275448e-07 * pow(x, 3) + 2.082790802069e- 10 * pow(x, 4) + -5,306931174991e-14 * pow(x, 5) + 4,787659214703e-18 * pow(x, 6); }

Zwróć uwagę na zmianę przecinka po kropce jako separatora dziesiętnego.

Krok 23: Przechwytywanie z poprawką - seria plotera

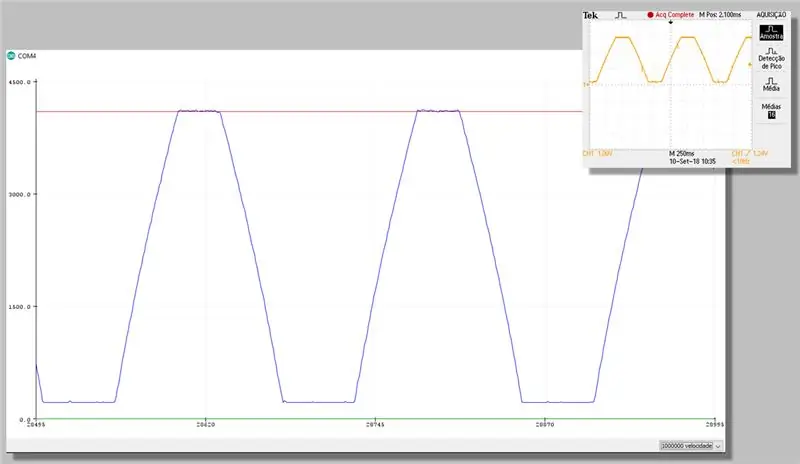
Krok 24: Koszt obliczeniowy

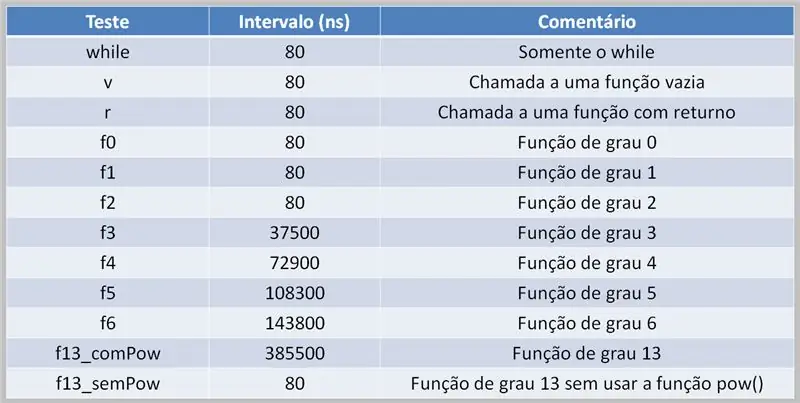
Aby wykonać obliczenia wielomianowe, procesor musi obsłużyć to zadanie. Może to prowadzić do opóźnień w wykonaniu, w zależności od kodu źródłowego i dostępnej mocy obliczeniowej.

Tutaj widzimy tabelę wyników testu z wielomianami wielostopniowymi. Zwróć uwagę na różnicę między czasami, w których funkcja pow() była używana, a czasami, kiedy jej nie używano.

Krok 25: Kod testowy - konfiguracja () i rozpoczęcie pętli ()

Tutaj mamy kod użyty w naszym teście.

void setup() { Serial.begin(1000000); //Zainicjuj porta szeregową część do debugowania } void loop() { float valor_analogico = 500.0; //um valor arbtrario float quantidade = 10000.0; //Quantidade de chamadas float contador = 0.0; //contador de chamadas

Krok 26: Kod testowy - pętla () i przetwarzanie

Użyłem funkcji micros(), aby uzyskać wartość w mikrosekundach.

//============= inicjacja procesu float agora = micros(); //marca o instante inicial while (contador < quantidade) { //v(valor_analogico); //função vazia //r(valor_analogico); //função com retorno //f0(valor_analogico); //grau 0 //f1(valor_analogico); //grau 1 //f2(valor_analogico); //grau 2 //f3(valor_analogico); //grau 3 //f4(valor_analogico); //grau 4 //f5(valor_analogico); //grau 5 //f6(valor_analogico); //grau 6 //f13_semPow(valor_analogico); //grau 13º SEM a função POW //f13_comPow(valor_analogico); //grau 13º COM a função POW contador++; } agora = (mikros() - agora) / ilość; //determina o intervalo que se passou para cada iteração //============= finaliza o processo

Krok 27: Kod testowy - Pętla () - Wyniki

Dla porównania drukujemy wartość zwróconą z funkcji grade 13 z POW i bez, a także interwał przetwarzania.

//imprime o valor retornado da função de grau 13 com e sem POW para comparação Serial.print(f13_semPow(valor_analogico)); //grau 13º SEM a função POW Serial.print(" - "); Serial.print(f13_comPow(valor_analogico)); //grau 13º COM a função POW Serial.print(" - "); //imprime o interwał do przetwarzania Serial.println(agora, 6); }

Krok 28: Kod testowy - używane funkcje

Puste funkcje (tylko ze zwrotem) stopnia 0 i 1.

//FUNÃO VAZIAdouble v(double x) { } //FUNÇÃO SOMENTE COM RETORNO double r(double x) { return x; } //FUNÇÃO DE GRAU 0 double f0(double x) { return 2.202196968876e+02; } //FUNÇÃO DE GRAU 1 podwójne f1(podwójne x) { powrót 2.202196968876e+02 + 3.561383996027e-01 * x; }

Funkcje klasy 2, 3 i 4.

//FUNÇÃO DE GRAU 2double f2(double x) { return 2.202196968876e+02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow(x, 2); } //FUNÇÃO DE GRAU 3 podwójne f3(podwójne x) { powrót 2.202196968876e+02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow(x, 2) + -3.470360275448e-07 * pow(x, 3); } //FUNÇÃO DE GRAU 4 podwójne f4(podwójne x) { powrót 2.202196968876e+02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow(x, 2) + -3.470360275448e-07 * pow(x, 3) + 2,082790802069e-10 * pow(x, 4); }

Funkcje klasy 5 i 6.

//FUNÇÃO DE GRAU 5double f5(double x) { powrót 2.202196968876e+02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow(x, 2) + -3.470360275448e-07 * pow(x, 3) + 2,082790802069e-10 * pow(x, 4) + -5,306931174991e-14 * pow(x, 5); } //FUNÇÃO DE GRAU 6 double f6(double x) { return 2.202196968876e+02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow(x, 2) + -3.470360275448e-07 * pow(x, 3) + 2,082790802069e-10 * pow(x, 4) + -5,306931174991e-14 * pow(x, 5) + 4,787659214703e-18 * pow(x, 6); }

Funkcja klasy 13 przy użyciu POW.

//FUNÇÃO DE GRAU 13 USANDO O POWdouble f13_comPow(double x) { return 2, 161282383460e+02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * pow(x, 2) + -3, 968558178426e-06 * pow(x, 3) + 1, 047910519933e-08 * pow(x, 4) + -1, 479271312313e-11 * pow(x, 5) + 1, 220894795714e-14 * pow(x, 6) + -6, 136200785076e-18 * pow(x, 7) + 1, 910015248179e-21 * pow(x, 8) + -3, 566607830903e-25 * pow(x, 9) + 5, 000280815521e-30 * pow(x, 10) + 3, 434515045670e-32 * pow(x, 11) + -1, 407635444704e-35 * pow(x, 12) + 9, 871816383223e-40 * pow(x, 13); }

Funkcja klasy 13 bez użycia POW.

//FUNÇÃO DE GRAU SEM USAR O POWdouble f13_semPow(double x) { powrót 2, 161282383460e+02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * x * x + -3, 968558178426e-06 * x * x * x + 1, 047910519933e-08 * x * x * x * x + -1, 479271312313e-11 * x * x * x * x * x + 1, 220894795714e-14 * x * x * x * x * x * x + -6, 136200785076e-18 * x * x * x * x * x * x * x + 1, 910015248179e-21 * x * x * x * x * x * x * x * x + -3, 566607830903e- 25 * x * x * x * x * x * x * x * x * x + 5, 000280815521e-30 * x * x * x * x * x * x * x * x * x * x + 3, 434515045670e- 32 * x * x * x * x * x * x * x * x * x * x * x + -1, 407635444704e-35 * x * x * x * x * x * x * x * x * x * x * x * x + 9, 871816383223e-40 * x * x * x * x * x * x * x * x * x * x * x * x * x; }

Krok 29: Pliki

Pobierz pliki:

PDF

JA NIE

Arkusz